题目内容
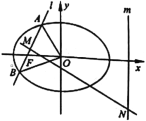
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的焦距为2,且经过点
的焦距为2,且经过点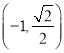 ,过左焦点
,过左焦点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() ,
,![]() ,
,![]() 的斜率之和为0,求直线
的斜率之和为0,求直线![]() 的方程;
的方程;
(3)设弦![]() 的垂直平分线分别与直线
的垂直平分线分别与直线![]() ,椭圆
,椭圆![]() 的右准线
的右准线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据已知求出![]() 的值,即得椭圆的
的值,即得椭圆的![]() 的方程;(2)设直线
的方程;(2)设直线![]() :
:![]() ,
,![]() ,联立直线和椭圆的方程得到韦达定理,根据直线
,联立直线和椭圆的方程得到韦达定理,根据直线![]() ,
,![]() ,
,![]() 的斜率之和为0,求出
的斜率之和为0,求出![]() ,即得直线的方程;(3)直线
,即得直线的方程;(3)直线![]() 的斜率不存在时,
的斜率不存在时,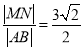 ;直线
;直线![]() 的斜率存在时,求出
的斜率存在时,求出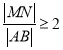 .即得解.
.即得解.
(1)因为椭圆![]() 的焦距为2,所以椭圆
的焦距为2,所以椭圆![]() 的焦点为
的焦点为![]() ,
,
所以点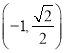 到焦点
到焦点![]() ,
,![]() 的距离分别为
的距离分别为![]() ,
,![]() ,
,
故![]() ,得
,得![]() .
.
所以![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)依题意,左焦点![]() ,设直线
,设直线![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() .
.
联立方程组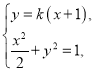 整理得
整理得![]() ,
,
所以![]() ,
,![]() .
.
因为直线![]() ,
,![]() ,
,![]() 的斜率之和为0,所以
的斜率之和为0,所以![]() ,
,
即![]() ,整理得
,整理得![]() ,
,
即![]() ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
(3)若直线![]() 的斜率不存在,
的斜率不存在,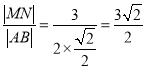 ;
;
若直线![]() 的斜率存在,由(2)可得
的斜率存在,由(2)可得![]()
![]()
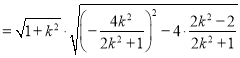
![]() ,
,
又![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,
所以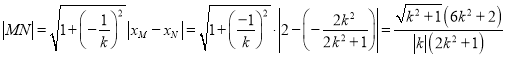 .
.
故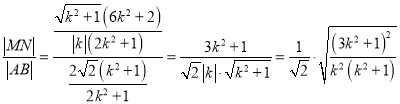 ,
,
令![]() ,则
,则![]() ,
,
故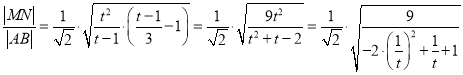
当![]() 时,
时,![]() ,
,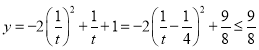 ,
,
所以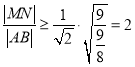 .
.
显然,![]() ,
,
所以![]() 的最小值为2.
的最小值为2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率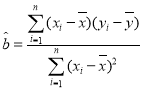 ;相关系数
;相关系数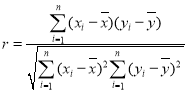 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |