题目内容
2. 某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为108πml.设圆柱的高度为hcm,底面半径半径为rcm,且h≥4r,假设该易拉罐的制造费用仅与其表面积有关,已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数)
某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为108πml.设圆柱的高度为hcm,底面半径半径为rcm,且h≥4r,假设该易拉罐的制造费用仅与其表面积有关,已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数)(1)写出易拉罐的制造费用y(元)关于r(cm)的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时r(cm)的值.
分析 (1)由题意,体积V=πr2h,可求得h,再由易拉罐的制造费用公式求得费用,根据函数得意义求得定义域.
(2)利用导数求出函数的单调区间,继而求得函数在定义域内的最值.
解答  解:(1)由题意,体积V=πr2h,得h=$\frac{V}{π{r}^{2}}=\frac{108}{{r}^{2}}$.
解:(1)由题意,体积V=πr2h,得h=$\frac{V}{π{r}^{2}}=\frac{108}{{r}^{2}}$.
y=2πrh×m+2πr2×n=2π ($\frac{108m}{r}$+nr2).…(4分)
因为h≥4r,即$\frac{108}{{r}^{2}}$≥4r,所以r≤3,即所求函数定义域为(0,3].…(6分)
(2)令f(r)=$\frac{108m}{r}$+nr2,则f'(r)=-$\frac{108m}{{r}^{2}}$+2nr.
由f'(r)=0,解得r=$3\root{3}{\frac{2m}{n}}$.
①若$3\root{3}{\frac{2m}{n}}$.<1,当n>2m时,$3\root{3}{\frac{2m}{n}}$.∈(0,3],由
| R | (0,$3\root{3}{\frac{2m}{n}}$). | $3\root{3}{\frac{2m}{n}}$. | ($3\root{3}{\frac{2m}{n}}$.,3] |
| f'(r) | - | 0 | + |
| f(r) | 减 | 增 |
②若$3\root{3}{\frac{2m}{n}}$.≥1,即n≤2m时,由f'(r)≤0知f(r)在(0,3]上单调递减,
当r=3时,f(r)有最小值,此时易拉罐制造费用最低.…(14分)
点评 本题主要考查导数在实际应用题中的应用,利用导数求得单调区间求出满足题意的结果.属于中档题型,在高考中时有考查.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
13.已知函数f(x)=|2x+1|+|2x-3|,若关于x的不等式f(x)<|a-1|的解集非空,则实数a的取值范围是( )
| A. | [-3,5] | B. | (-3,5) | C. | (-∞,-3]∪[5,+∞) | D. | (-∞,-3)∪(5,+∞) |
12.一个四棱锥的侧棱长都相等,底面是正方形,其主视图如图所示,该四棱锥侧面积等于( )

| A. | 20 | B. | 5$\sqrt{2}$ | C. | 4($\sqrt{5}$+1) | D. | 4$\sqrt{5}$ |
 对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为100.
对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为100.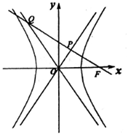 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.