题目内容
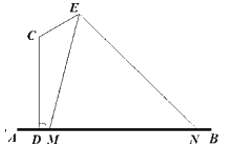
【题目】如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=![]() ,.计划在
,.计划在![]() 上再建一座观赏亭P,记∠POB=θ
上再建一座观赏亭P,记∠POB=θ![]() .
.
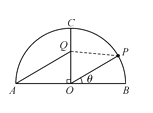
(1)当θ=![]() 时,求∠OPQ的大小;
时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)设∠OPQ=α,在△POQ中,用正弦定理![]() 可得含α,θ的关系式,将其展开化简并整理后得tanα=
可得含α,θ的关系式,将其展开化简并整理后得tanα=![]() ,将θ=
,将θ=![]() 代入得答案;
代入得答案;
(2)令f(θ)=![]() 并利用导数求得f(θ)的最大值,即此时的
并利用导数求得f(θ)的最大值,即此时的![]() ,由(1)可知tanα=
,由(1)可知tanα=![]() ,得答案.
,得答案.
(1)设∠OPQ=α,在△POQ中,用正弦定理可得含α,θ的关系式.
因为∠AQC=![]() ,所以∠AQO=
,所以∠AQO=![]() .又OA=OB=3,所以OQ=
.又OA=OB=3,所以OQ=![]()
在△OPQ中,OQ=![]() ,OP=3,∠POQ=
,OP=3,∠POQ=![]() -θ,设∠OPQ=α,则∠PQO=
-θ,设∠OPQ=α,则∠PQO=![]() -α+θ.
-α+θ.
由正弦定理,得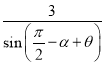 =
=![]() ,即
,即![]() sinα=cos(α-θ).
sinα=cos(α-θ).
展开并整理,得tanα=![]() ,其中θ∈
,其中θ∈![]() .
.
此时当θ=![]() 时,tanα=
时,tanα=![]() .因为α∈(0,π),所以α=
.因为α∈(0,π),所以α=![]() .
.
故当θ=![]() 时,∠OPQ=
时,∠OPQ=![]() .
.
(2)设f(θ)=![]() ,θ∈
,θ∈![]() .
.
则f′(θ)=![]() =
=![]() .
.
令f′(θ)=0,得sinθ=![]() ,记锐角θ0满足
,记锐角θ0满足![]() ,
,
则![]() ,即
,即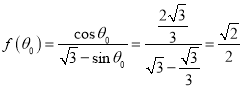
列表如下:
θ | (0,θ0) | θ0 |
|
f′(θ) | + | 0 | - |
f(θ) | 单调递增 |
| 单调递减 |
由上表可知,f(θ0)=![]() 是极大值,也是最大值.
是极大值,也是最大值.
由(1)可知tanα=f(θ)>0,则![]() , tanα单调递增
, tanα单调递增
则当tanα取最大值![]() 时,α也取得最大值.
时,α也取得最大值.
故游客在观赏亭P处的观赏效果最佳时,sinθ=![]() .
.

练习册系列答案
相关题目