题目内容
【题目】某无缝钢管厂只生产甲、乙两种不同规格的钢管,钢管有内外两个口径,甲种钢管内外两口径的标准长度分别为![]() 和
和![]() ,乙种钢管内外两个口径的标准长度分别为
,乙种钢管内外两个口径的标准长度分别为![]() 和
和![]() .根据长期的生产结果表明,两种规格钢管每根的长度
.根据长期的生产结果表明,两种规格钢管每根的长度![]() 都服从正态分布
都服从正态分布![]() ,长度在
,长度在![]() 之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
(1)在该钢管厂生产的钢管中随机抽取10根进行检测,求至少有1根为废品的概率;
(2)监管部门规定每种规格钢管的“口径误差”的计算方式为:若钢管的内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() ,则“口径误差”为
,则“口径误差”为![]() ,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是
,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是![]() (正品钢管中没有“口径误差”大于
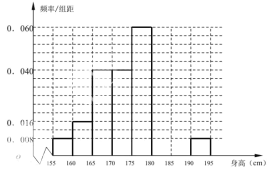
(正品钢管中没有“口径误差”大于![]() 的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
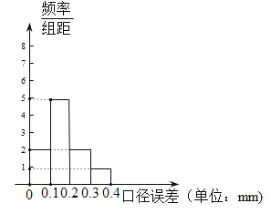

甲种钢管 乙种钢管
已知经销商经销甲种钢管,其中“一级品”的利润率为0.3,“二级品”的利润率为0.18,“合格品”的利润率为0.1;经销乙种钢管,其中“一级品”的利润率为0.25,“二级品”的利润率为0.15,“合格品”的利润率为0.08,若视频率为概率.
(ⅰ)若经销商对甲、乙两种钢管各进了100万元的货,![]() 和
和![]() 分别表示经销甲、乙两种钢管所获得的利润,求
分别表示经销甲、乙两种钢管所获得的利润,求![]() 和
和![]() 的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
(ⅱ)若经销商计划对甲、乙两种钢管总共进100万元的货,则分别在甲、乙两种钢管上进货多少万元时,可使得所获利润的方差和最小?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ,
,![]() ,
,![]() ,利弊见解析;(ⅱ)甲种钢管上投资25万元,在乙种钢管上投资75万元
,利弊见解析;(ⅱ)甲种钢管上投资25万元,在乙种钢管上投资75万元
【解析】
(1)结合题意,由正态分布的概率进行计算即可;
(2)(ⅰ)根据题意,求解分布列,再根据分布列求解期望和方差即可;
(ⅱ)构造方差和的函数,根据方差的运算性质,利用已知求函数的最小值即可.
(1)由正态分布可知,抽取的1根钢管的长度在![]() 之内的概率为0.9974,
之内的概率为0.9974,
则这10根钢管的长度全在![]() 内的概率为
内的概率为![]() ,
,
则这10根中至少有1根为废品的概率约为![]() .
.
(2)(ⅰ)由利润率和投额可得![]() 可为30万元、18万元、10万元,
可为30万元、18万元、10万元,
![]() 可为25万元、15万元、8万元.
可为25万元、15万元、8万元.
又由直方图可得对应的频率为0.2、0.5、0.3和0.2、0.8、0,
所以随机变量![]() 的分布列为
的分布列为
| 30 | 18 | 10 |
| 0.2 | 0.5 | 0.3 |
![]() (万元),
(万元),
![]() .
.
随机变量![]() 的分布列为
的分布列为
| 25 | 15 | 8 |
| 0.2 | 0.8 | 0 |
![]() (万元),
(万元),![]() .
.
经销商经销甲种钢管的平均利润18万元大于经销乙种钢管的平均利润17万元,
但经销甲种钢管的方差48大于经销乙种钢管的方差16.
所以经销甲种钢管的平均利润大,方差也大,相对不稳定;
而经销乙种钢管的平均利润小,方差也小,相对稳定.
(ⅱ)设经销商进了![]() 万元的甲种钢管,则进了
万元的甲种钢管,则进了![]() 万元的乙种钢管,
万元的乙种钢管,
令![]() 为经销甲种钢管所获利润的方差与经销乙种钢管所获利润的方差的和,则
为经销甲种钢管所获利润的方差与经销乙种钢管所获利润的方差的和,则
![]()
![]()
![]()
![]() .
.
当![]() 时,
时,![]() 的值最小.
的值最小.
故在甲种钢管上投资25万元,在乙种钢管上投资75万元时,
可使经销甲种钢管所获利润的方差与经销乙种钢管所获利润的方差和最小.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案