题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若关于![]() 的方程
的方程![]() 只有一个实数解,求实数
只有一个实数解,求实数![]() 的取值范围;
的取值范围;
(2)若当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)方程![]() 可化为
可化为![]() ,易知
,易知![]() 已是该方程的根,从而要使原方程只有一解,即要求方程
已是该方程的根,从而要使原方程只有一解,即要求方程![]() 有且仅有一个等于1的解或无解,结合图象可得a的范围;
有且仅有一个等于1的解或无解,结合图象可得a的范围;
(2)不等式![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,分
恒成立,分![]() ,
,![]() 两种情况进行讨论,分离出参数a后转化为求函数的最值即可;
两种情况进行讨论,分离出参数a后转化为求函数的最值即可;
(1)方程![]() ,即
,即![]() ,变形得
,变形得![]() ,
,
显然,![]() 已是该方程的根,从而欲使原方程只有一解,即要求方程
已是该方程的根,从而欲使原方程只有一解,即要求方程![]() 有且仅有一个等于1的解或无解,
有且仅有一个等于1的解或无解,
![]() .即
.即![]() 的取值范围是
的取值范围是![]() .
.
(2)当![]() 时,不等式
时,不等式![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立.
恒成立.
①当![]() 时,
时,![]() 式显然成立,此时
式显然成立,此时![]() .
.
②当![]() 时,
时,![]() 式可变形为
式可变形为![]()
令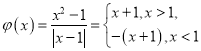
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,故此时
,故此时![]() .
.
综合①②,得所求实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




