题目内容
设数列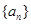 的前
的前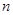 项和为
项和为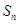 ,且满足
,且满足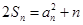 ,
,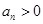 ,
,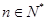 .
.
(1)猜想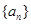 的通项公式,并加以证明;
的通项公式,并加以证明;
(2)设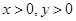 ,且
,且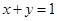 ,证明:
,证明: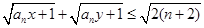 .
.
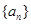 的前
的前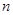 项和为
项和为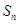 ,且满足
,且满足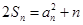 ,
,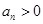 ,
,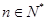 .
.(1)猜想
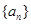 的通项公式,并加以证明;
的通项公式,并加以证明;(2)设
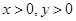 ,且
,且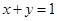 ,证明:
,证明: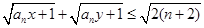 .
.(1)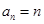 ,见解析;(2)见解析.
,见解析;(2)见解析.
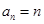 ,见解析;(2)见解析.
,见解析;(2)见解析.(1)利用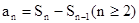 公式化简得出关于数列的递推式子,再结合等差数列的概念求出通项公式;(2)利用分析法和均值不等式易证
公式化简得出关于数列的递推式子,再结合等差数列的概念求出通项公式;(2)利用分析法和均值不等式易证
解:(1)分别令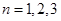 ,得
,得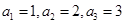 ,猜想得
,猜想得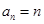 (3分)
(3分)
法一:数学归纳法按步给分
法二:由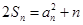 ,得
,得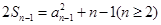 ,两式作差得,
,两式作差得,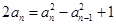
即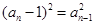
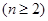 (6分)
(6分)
∵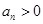 ∴
∴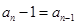 ,即
,即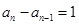
∴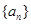 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴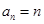 (9分)
(9分)
(2)要证 ,只要证
,只要证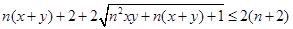
代入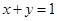 ,即证
,即证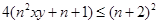 即证
即证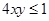 (13分)
(13分)
∵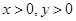 ,且
,且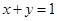 ∴
∴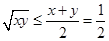 即
即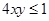 得证(15分)
得证(15分)
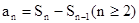 公式化简得出关于数列的递推式子,再结合等差数列的概念求出通项公式;(2)利用分析法和均值不等式易证
公式化简得出关于数列的递推式子,再结合等差数列的概念求出通项公式;(2)利用分析法和均值不等式易证解:(1)分别令
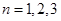 ,得
,得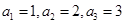 ,猜想得
,猜想得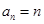 (3分)
(3分)法一:数学归纳法按步给分
法二:由
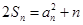 ,得
,得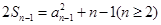 ,两式作差得,
,两式作差得,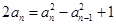
即
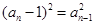
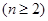 (6分)
(6分)∵
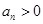 ∴
∴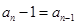 ,即
,即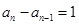
∴
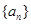 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴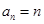 (9分)
(9分)(2)要证
 ,只要证
,只要证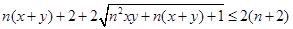
代入
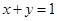 ,即证
,即证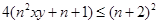 即证
即证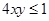 (13分)
(13分)∵
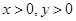 ,且
,且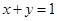 ∴
∴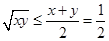 即
即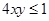 得证(15分)
得证(15分)
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
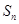 是正项数列
是正项数列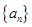 的前
的前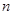 项和,且
项和,且 (
(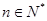 ).
).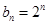 ,设
,设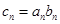 ,求数列
,求数列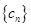 的前
的前 .
.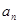 )满足
)满足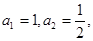 并且
并且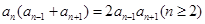 ,则数列的第2012项为
,则数列的第2012项为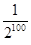
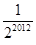
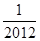
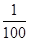
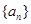 的公差
的公差 ,若
,若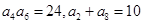 ,则该数列的前
,则该数列的前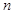 项和
项和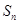 的最大值为( )
的最大值为( )
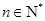 ,
,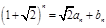 (
(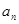 、
、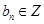 ).
).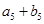 的值; (2)求证:数列
的值; (2)求证:数列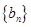 各项均为奇数.
各项均为奇数.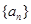 是一个等差数列,且
是一个等差数列,且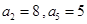 .等比数列
.等比数列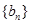 的前
的前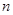 项和为
项和为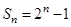 .
.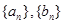 的通项公式;
的通项公式;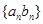 的最大项及相应
的最大项及相应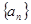 中,
中, 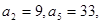 则
则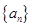 的前n项和为
的前n项和为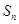 ,若
,若 则
则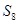 = ;
= ;