Question

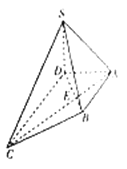
【题目】如图，在四棱锥中，，∠ABD=∠ADB.

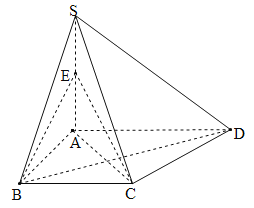
（Ⅰ）求证：；

（Ⅱ）若，，，，，点为的中点，求平面切割三棱锥得到的上下两个几何体的体积之比.

Answer 1

【答案】（Ⅰ）证明见解析（Ⅱ）

【解析】

（Ⅰ）取BD中点F，连接AF，SF，由已知可得SF⊥BD，AF⊥BD，再由线面垂直的判定可得BD⊥平面SAF，则SA⊥BD；

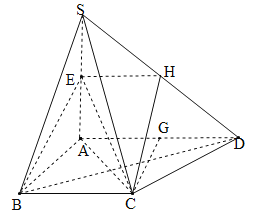
（Ⅱ）取SD中点H，连接CH，EH，可得EH∥BC，故B，C，E，H共面，过C作CG⊥AD于G，设AB=x，由tan∠CDA=2求得x=2，证明AB⊥平面SAD，然后分别求出三棱锥S-ACD与四棱锥C-AEHD的体积，则答案可求．

（Ⅰ）取的中点，连接，．

∵，∴，

∵，∴．

∵，∴，

∵，∴．

∵，平面，平面，

∴平面．

∵平面，∴．

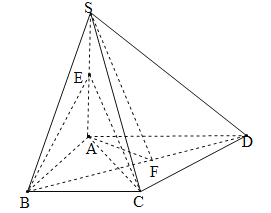
（Ⅱ）取的中点，连接，，

易知，故点共面．

过作于．

设，故，解得．

又，，，

∴平面．

∴，．

∴，∴．