题目内容
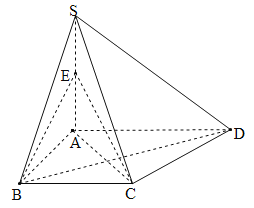
【题目】如图,在四棱锥![]() 中,
中,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ,并证明你的结论;
,并证明你的结论;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(I)取线段![]() 上靠近
上靠近![]() 的三等分点
的三等分点![]() ,连接
,连接![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() ,由
,由![]() ,得
,得![]() ,所以
,所以![]() ,即可证明结论成立.
,即可证明结论成立.
(II)以![]() 为坐标原点,以直线
为坐标原点,以直线![]() 分别为
分别为![]() 轴,过点
轴,过点![]() 且与
且与![]() 平面垂直的直线为
平面垂直的直线为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的个法向量为
的个法向量为![]() ,由向量法即可求出二面角的平面角.
,由向量法即可求出二面角的平面角.
(I)取线段![]() 上靠近
上靠近![]() 的三等分点
的三等分点![]() ,连接
,连接![]() .因为
.因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() .而
.而![]() ,所以
,所以![]() ,所以
,所以![]() .而
.而![]() 平面
平面![]() .
.![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(II)易知 ![]()
![]() 为等边三角形,所以
为等边三角形,所以![]() .又
.又![]() ,故
,故![]() ,所以有
,所以有![]() .由已知可得
.由已知可得![]() ,又
,又![]() ,所以
,所以![]() 平面
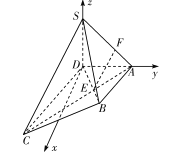
平面![]() .以
.以![]() 为坐标原点,以直线
为坐标原点,以直线![]() 分别为
分别为![]() 轴,过点
轴,过点![]() 且与
且与![]() 平面垂直的直线为
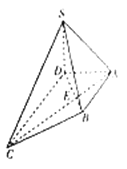
平面垂直的直线为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
设![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有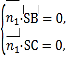 即
即
设![]() ,则
,则![]() ,所以
,所以![]() .
.
设平面![]() 的个法向量为
的个法向量为![]() ,则有
,则有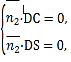 即
即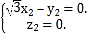
令![]() ,则
,则![]() ,所以
,所以![]() .
.
所以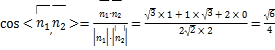 .
.
因为二面角![]() 为锐角,故所求二面角的余弦值为
为锐角,故所求二面角的余弦值为![]() .
.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】某校开展“我身边的榜样”评选活动,现对3名候选人甲、乙、丙进行不记名投票,投票要求详见选票.这3名候选人的得票数(不考虑是否有效)分别为总票数的88%,75%,46%,则本次投票的有效率(有效票数与总票数的比值)最高可能为百分之________.
“我身边的榜样”评选选票 | ||
候选人 | 符号 | 注: 1.同意画“○”,不同意画“×”. 2.每张选票“○”的个数不超过2时才为有效票. |
甲 | ||
乙 | ||
丙 | ||