Question

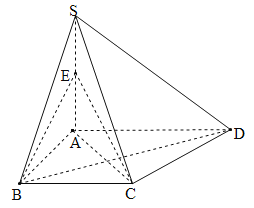
【题目】如图，在四棱锥中，平面，底面是正形，，为的中点．

（1）求证：平面；

（2）求二面角的余弦值．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）推导出DE⊥PC，BC⊥CD，BC⊥PD，从而BC⊥平面PCD，进而DE⊥BC，由此能证明DE⊥平面PCB.
（2）以D为原点，DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系，利用向量法能求出二面角EDBP的余弦值.

解：（1）证明：∵在四棱锥PABCD中，PD⊥平面ABCD，
底面ABCD是正方形，PD＝AB，E为PC的中点，
∴DE⊥PC，BC⊥CD，BC⊥PD，
∵PD∩CD＝D，

∴BC⊥平面PCD，
∵DE平面PCD，

∴DE⊥BC，
∵PC∩BC＝C，

∴DE⊥平面PCB；
（2）解：以D为原点，DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系，
设PD＝AB＝2，

则E（0，1，1），B（2，2，0），D（0，0，0），P（0，0，2），
，
设平面BDE的法向量，
则，取，得，
设平面BDP的法向量，
则，取，得，
设二面角EBDP的平面角为θ.
则.
∴二面角EBDP的余弦值为.