题目内容
设f(x)是定义在[-1,1]上的奇函数,且对任意a、b∈[-1,1],当a+b≠0时,都有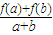 >0.
>0.(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x-
 )<f(x-
)<f(x- );
);(3)记P={x|y=f(x-c)},Q={x|y=f(x-c2)},且P∩Q=∅,求c的取值范围.
【答案】分析:先判断函数的单调性.
(1)由函数的单调性即可求解.
(2)(3)由函数的定义域及函数的单调性求解.
解答:解:设-1≤x1<x2≤1,则x1-x2≠0,
∴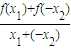 >0.
>0.
∵x1-x2<0,∴f(x1)+f(-x2)<0.
∴f(x1)<-f(-x2).
又f(x)是奇函数,∴f(-x2)=-f(x2).
∴f(x1)<f(x2).
∴f(x)是增函数.
(1)∵a>b,∴f(a)>f(b).
(2)由f(x- )<f(x-
)<f(x- ),得
),得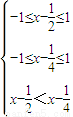 ∴-
∴- ≤x≤
≤x≤ .
.
∴不等式的解集为{x|- ≤x≤
≤x≤ }.
}.
(3)由-1≤x-c≤1,得-1+c≤x≤1+c,
∴P={x|-1+c≤x≤1+c}.
由-1≤x-c2≤1,得-1+c2≤x≤1+c2,
∴Q={x|-1+c2≤x≤1+c2}.
∵P∩Q=∅,
∴1+c<-1+c2或-1+c>1+c2,
解得c>2或c<-1.
点评:本题主要考查了函数单调性的应用,但应注意函数的定义域,在定义域内求解.
(1)由函数的单调性即可求解.
(2)(3)由函数的定义域及函数的单调性求解.
解答:解:设-1≤x1<x2≤1,则x1-x2≠0,
∴
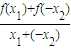 >0.
>0.∵x1-x2<0,∴f(x1)+f(-x2)<0.
∴f(x1)<-f(-x2).
又f(x)是奇函数,∴f(-x2)=-f(x2).
∴f(x1)<f(x2).
∴f(x)是增函数.
(1)∵a>b,∴f(a)>f(b).
(2)由f(x-
 )<f(x-
)<f(x- ),得
),得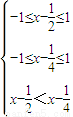 ∴-
∴- ≤x≤
≤x≤ .
.∴不等式的解集为{x|-
 ≤x≤
≤x≤ }.
}.(3)由-1≤x-c≤1,得-1+c≤x≤1+c,
∴P={x|-1+c≤x≤1+c}.
由-1≤x-c2≤1,得-1+c2≤x≤1+c2,
∴Q={x|-1+c2≤x≤1+c2}.
∵P∩Q=∅,
∴1+c<-1+c2或-1+c>1+c2,
解得c>2或c<-1.
点评:本题主要考查了函数单调性的应用,但应注意函数的定义域,在定义域内求解.

练习册系列答案
相关题目
 设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2013)+f(2014)=( )
设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2013)+f(2014)=( )