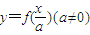题目内容

例2．设f（x）是定义在[-3，
2
]上的函数，求下列函数的定义域（1）y=f(
x
-2)（2）y=f(
x
a
)(a≠0)
分析：利用x∈[-3，
2
]，分别求出
x
-2∈[-3，
2
]，
x
a
∈[-3，
2
]，的解集，就是（1）y=f(
x
-2)（2）y=f(
x
a
)(a≠0)的定义域．
解答：解：（1）因为f（x）是定义在[-3，
2
]上的函数，对于y=f(
x
-2)，
所以
x
-2∈[-3，
2
]
解得-（6+2
2
）≤x≤6+2
2
，所以y=f(
x
-2)的定义域：[-6-2
2
，6+2
2
]
（2）因为f（x）是定义在[-3，
2
]上的函数，对于y=f(
x
a
)(a≠0)，有
x
a
∈[-3，
2
]
当a＞0时，y=f(
x
a
)(a≠0)的定义域：[-2a2，2a2]
当a＜0时，y=f(
x
a
)(a≠0)的定义域：[-9a2，9a2]
（3）y=f（2x）+f（x+m）  （m＞0）
点评：本题考查函数的定义域及其求法，考查计算能力，分类讨论思想是基础题．
练习册系列答案
相关题目
（1）设f（x）是定义在R上奇函数，且当x＞0时，f（x）=2x-3，则当x＜0时，f（x）表达式为
 
．
（2）设f（x）是定义在R上奇函数，且f（x+1）=-f（x），当x∈（0，1）时，f（x）=2x-3，则x∈（3，4）时，f（x）表达式为
 
．
已知函数f(x)=log
1
2
x与函数g（x）的图象关于y=x对称，
（1）若g（a）g（b）=2，且a＜0，b＜0，则
4
a
+
1
b
的最大值为
-9
-9

（2）设f（x）是定义在R上的偶函数，对任意的x∈R，都有f（2-x）=f（x+2），且当x∈[-2，0]时，f（x）=g（x）-1，若关于x的方程f（x）-lo
g
(x+2)
a
=0（a＞1）在区间（-2，6]内恰有三个不同实根，则实数a的取值范围是
(
34
，2)
(
34
，2)
．
设f（x）是定义在集合D上的函数，若对集合D中的任意两数x1，x2恒有f(
1
4
x1+
3
4
x2)＜
1
4
f(x1)+
3
4
f(x2)成立，则f（x）是定义在D上的β函数．
（1）试判断f（x）=x2是否是其定义域上的β函数？
（2）设f（x）是定义在R上的奇函数，求证：f（x）不是定义在R上的β函数．
（3）设f（x）是定义在集合D上的函数，若对任意实数α∈[0，1]以及集合D中的任意两数x1，x2恒有f（αx1+（1-α）x2）≤αf（x1）+（1-α）f（x2），则称f（x）是定义在D上的α-β函数．已知f（x）是定义在R上的α-β函数，m是给定的正整数，设an=f（n），n=1，2，3…m且a0=0，am=2m，记∫=a1+a2+a3+…+am，对任意满足条件的函数f（x），求∫的最大值．
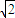例2．设f（x）是定义在[-3，]上的函数，求下列函数的定义域（1）（2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网