题目内容
(2013•内江一模)设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x-2)=f(x+2)且当x∈[-2,0]时,f(x)=(
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
| 1 |
| 2 |
(
,2)
| 3 | 4 |
(
,2)
.| 3 | 4 |
分析:由已知中可以得到函数f(x)是一个周期函数,且周期为4,将方程f(x)-logax+2=0恰有3个不同的实数解,转化为
函数f(x)的与函数y=-logax+2的图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
函数f(x)的与函数y=-logax+2的图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
解答:解:∵对于任意的x∈R,都有f(x-2)=f(2+x),∴函数f(x)是一个周期函数,且T=4.
又∵当x∈[-2,0]时,f(x)=(
)x-1,且函数f(x)是定义在R上的偶函数,
若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
则函数y=f(x)与y=loga(x+2)在区间(-2,6]上有三个不同的交点,如下图所示:
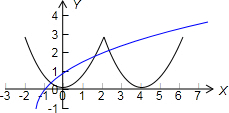
又f(-2)=f(2)=3,则有 loga4<3,且loga8>3,解得:
<a<2,
故答案为 (
,2).
又∵当x∈[-2,0]时,f(x)=(
| 1 |
| 2 |
若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
则函数y=f(x)与y=loga(x+2)在区间(-2,6]上有三个不同的交点,如下图所示:

又f(-2)=f(2)=3,则有 loga4<3,且loga8>3,解得:
| 3 | 4 |
故答案为 (
| 3 | 4 |
点评:本题考查的知识点是根的存在性及根的个数判断,指数函数与对数函数的图象与性质,其中根据方程的解与函数的零点之间的关系,将方程根的问题转化为函数零点问题,是解答本题的关键,体现了转化和数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
 (2013•内江一模)如图茎叶图表示的是甲,乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为
(2013•内江一模)如图茎叶图表示的是甲,乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为 (2013•内江一模)武汉市为增强市民交通安全意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组
(2013•内江一模)武汉市为增强市民交通安全意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组