题目内容
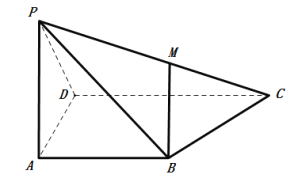
【题目】如图所示，已知ABCD为梯形，AB∥CD，CD=2AB，M为线段PC上一点.
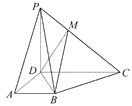
(1)设平面PAB∩平面PDC=l，证明：AB∥l；
(2)在棱PC上是否存在点M，使得PA∥平面MBD，若存在，请确定点M的位置；若不存在，请说明理由.
【答案】（1）见解析；（2）存在，
【解析】
试题分析:(1) 因为AB∥CD,根据线面平行的判定定理可得AB∥平面PCD，再根据线面平行的性质定理证出结论;(2) 存在点M，使得PA∥平面MBD，此时
=
. 连接AC交BD于点O，连接MO. 因为AB∥CD，且CD=2AB，所以
=
=，又因为=，可得PA∥MO，根据线面平行的判定定理证出结论.
试题解析:
(1)因为AB∥CD，AB平面PCD，CD平面PCD，
所以AB∥平面PCD，又因为平面PAB∩平面PDC=l，且AB平面PAB，
所以AB∥l.
(2)存在点M，使得PA∥平面MBD，此时=.证明如下：连接AC交BD于点O，连接MO.
因为AB∥CD，且CD=2AB，所以==，又因为=，PC∩AC=C，
所以PA∥MO，因为PA平面MBD，MO平面MBD，所以PA∥平面MBD.
练习册系列答案
相关题目
