题目内容
【题目】某医疗研究所为了检验某种血清预防感冒的作用，把
名使用血清的人与另外名未用血清的人一年中的感冒记录作比较，提出假设
：“这种血清不能起到预防感冒的作用”，利用
列联表计算得
，经查对临界值表知
．对此，四名同学做出了以下的判断：
：有
的把握认为“这种血清能起到预防感冒的作用”
：若某人未使用该血清，那么他在一年中有的可能性得感冒
：这种血清预防感冒的有效率为
：这种血清预防感冒的有效率为
则下列结论中，正确结论的序号是
①
； ②
； ③
； ④
【答案】①④
【解析】
解：查对临界值表知
，
故有95%的把握认为“这种血清能起到预防感冒的作用”
95%仅是指“血清与预防感冒”可信程度，
但也有“在100个使用血清的人中一个患感冒的人也没有”的可能．
故
真，其余都假．结合复合命题的真值可知，选①④
练习册系列答案
相关题目
【题目】已知某校5个学生的数学和物理成绩如下：
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学成绩 | 80 | 75 | 70 | 65 | 60 |
物理成绩 | 70 | 66 | 68 | 64 | 62 |
（1）通过大量事实证明发现，一个学生的数学成绩和物理成绩是具有很强的线性相关关系的，在上述表格中，用
表示数学成绩，用
表示物理成绩，求关于的回归方程．
（2）利用残差分析回归方程的拟合效果，若残差和在
范围内，则称回归方程为“优拟方程”，问：该回归方程是否为“优拟方程”．
（3）现从5名同学中任选两人参加访谈活动，求1号同学没被选中的概率.
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为：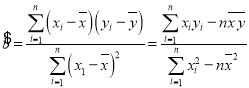
，
.
