题目内容
【题目】已知函数 ![]() .
.
(1)设函数h(x)=g(x)﹣f(x),求函数h(x)在区间[2,4]上的值域;
(2)定义min(p,q)表示p,q中较小者,设函数H(x)=min{f(x),g(x)}(x>0), ①求函数H(x)的单调区间及最值;
②若关于x的方程H(x)=k有两个不同的实根,求实数k的取值范围.
【答案】
(1)解:∵函数f(x)在区间(0,+∞)上单调递减,
函数g(x)在区间(0,+∞)上单调递增,
∴函数h(x)在区间[2,4]上单调递增,
故h(2)≤h(x)≤h(4),即0≤h(x)≤13,
所以函数在区间[2,4]上的值域为[0,13]
(2)解:①在同一坐标系中,作出f(x),g(x)的图象如图所示,
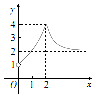
根据题意得,H(x)= 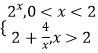 ,
,
由(1)知,y=2x在区间(0,2]上单调递增,
![]() 在区间上单调递减,
在区间上单调递减,
故H(x)max=H(2)=4.
∴函数H(x)的单调递增区间为(0,2],单调递减区间为(2,+∞),
H(x)有最大值4,无最小值.
②∵ ![]() 在[2,+∞)上单调递减,∴
在[2,+∞)上单调递减,∴ ![]() ,
,
又g(x)=2x在(0,2]上单调递增,∴1<2x≤4,
∴要使方程H(x)=k有两个不同的实根,
则需满足2<k<4,
即实数k的取值范围是(2,4)
【解析】(1)根据函数f(x),g(x)的单调性,求出h(x)的单调性,求出函数h(x)的值域即可;(2)①根据函数f(x),g(x)的图象求出H(x)的最大值,②根据H(x)的范围,求出k的范围即可.
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求a,b,c的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
