题目内容
【题目】已知函数 ![]() ,若满足f(1)=
,若满足f(1)= ![]()
(1)求实数a的值;
(2)证明:f(x)为奇函数.
(3)判断并证明函数f(x)的单调性.
【答案】
(1)解:f(1)= ![]() ;
;
∴ ![]() ;
;
∴a=1
(2)解:证明: ![]() ;
;
该函数定义域为R,f(﹣x)= ![]() ;
;
∴f(x)为奇函数
(3)解: ![]() ,可看出x增大时,f(x)增大,∴f(x)在R上为增函数,证明如下:
,可看出x增大时,f(x)增大,∴f(x)在R上为增函数,证明如下:
设x1,x2∈R,且x1<x2,则:
![]() =
= ![]() ;
;
∵x1<x2;
∴ ![]() ,
, ![]() ;
;
∴f(x1)<f(x2);
∴f(x)在R上为增函数
【解析】(1)根据f(1)= ![]() 便可求出a=1;(2)写出
便可求出a=1;(2)写出 ![]() ,定义域显然为R,容易得到f(﹣x)=﹣f(x),从而得出该函数为奇函数;(3)分离常数得到
,定义域显然为R,容易得到f(﹣x)=﹣f(x),从而得出该函数为奇函数;(3)分离常数得到 ![]() ,根据单调性定义便可判断该函数在R上单调递增,根据增函数的定义证明:设任意的x1 , x2∈R,且x1<x2 , 然后作差,通分,根据指数函数的单调性证明f(x1)<f(x2)即可得出f(x)在R上单调递增.
,根据单调性定义便可判断该函数在R上单调递增,根据增函数的定义证明:设任意的x1 , x2∈R,且x1<x2 , 然后作差,通分,根据指数函数的单调性证明f(x1)<f(x2)即可得出f(x)在R上单调递增.
【考点精析】利用函数单调性的判断方法和函数奇偶性的性质对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

 优学名师名题系列答案
优学名师名题系列答案【题目】2017年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如下表:
评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
评分类型 | D | C | B | A |
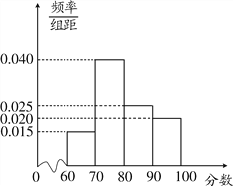 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.