Question

【题目】为实现2020年全面建设小康社会，某地进行产业的升级改造.经市场调研和科学研判，准备大规模生产某高科技产品的一个核心部件，目前只有甲、乙两种设备可以独立生产该部件.如图是从甲设备生产的部件中随机抽取400件，对其核心部件的尺寸x，进行统计整理的频率分布直方图.

根据行业质量标准规定，该核心部件尺寸x满足：|x﹣12|≤1为一级品，1＜|x﹣12|≤2为二级品，|x﹣12|＞2为三级品.

（Ⅰ）现根据频率分布直方图中的分组，用分层抽样的方法先从这400件样本中抽取40件产品，再从所抽取的40件产品中，抽取2件尺寸x∈[12，15]的产品，记ξ为这2件产品中尺寸x∈[14，15]的产品个数，求ξ的分布列和数学期望；

（Ⅱ）将甲设备生产的产品成箱包装出售时，需要进行检验.已知每箱有100件产品，每件产品的检验费用为50元.检验规定：若检验出三级品需更换为一级或二级品；若不检验，让三级品进入买家，厂家需向买家每件支付200元补偿.现从一箱产品中随机抽检了10件，结果发现有1件三级品.若将甲设备的样本频率作为总体的慨率，以厂家支付费用作为决策依据，问是否对该箱中剩余产品进行一一检验？请说明理由；

（Ⅲ）为加大升级力度，厂家需增购设备.已知这种产品的利润如下：一级品的利润为500元/件；二级品的利润为400元/件；三级品的利润为200元/件.乙种设备产品中一、二、三级品的概率分别是，，.若将甲设备的样本频率作为总体的概率，以厂家的利润作为决策依据.应选购哪种设备？请说明理由.

Answer 1

【答案】（Ⅰ）分布列见解析，；（Ⅱ）不对剩余产品进行逐一检验，理由见解析；（Ⅲ）应选购乙设备，理由见解析.

【解析】

（I）利用频率分布直方图中的频率（概率）求出尺寸在的产品件数，及在的产品件数，得ξ的可能取值为0，1，2，分别计算出概率得概率分布列，由分布列计算出期望；

（II）三级品的概率为（0.1+0.075）×1=0.175，计算对剩余产品逐一检验和对剩余产品不检验需支付的费用，比较后可得；

（III）利用频率（概率）计算出两种方案的利润期望，比较可得．

（I）抽取的40件产品中，产品尺寸x∈[12，15]的件数为：40×[（0.2+0.175+0.075）×1]=18，

其中x∈[14，15]的产品件数为40×（0.075×1）=3，

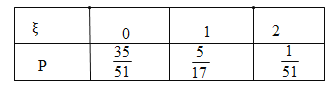
∴ξ的可能取值为0，1，2，

∴P（ξ=0），P（ξ=1），P（ξ=2），

∴ξ的分布列为：

∴Eξ＝012.

（II）三级品的概率为（0.1+0.075）×1=0.175，

若对剩余产品逐一检验，则厂家需支付费用50×100=5000；

若对剩余产品不检验，则厂家需支付费用50×10+200×90×0.175=3650，

∵5000＞3650，

故不对剩余产品进行逐一检验.

（III）设甲设备生产一件产品的利润为y1，乙设备生产一件产品的利润为y2，

则E（y1）=500×（0.3+0.2）+400×（0.150+0.175）+200×0.175=415，

E（y2）=500400200420.

∵E（y1）＜E（y2）.

∴应选购乙设备.