题目内容
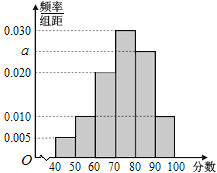
【题目】东莞的轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内(含4小时)每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内(含24小时)收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次),得到下面的频数分布表:

以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的![]() 列联表:
列联表:

完成上述列联表,并判断能否有![]() 的把握认为“停车是否超过6小时”与性别有关?
的把握认为“停车是否超过6小时”与性别有关?
(2)(i)X表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求X的概率分布列及期望![]() :
:
(ii)现随机抽取该停车场内停放的3辆车,![]() 表示3辆车中停车费用大于
表示3辆车中停车费用大于![]() 的车辆数,求P(
的车辆数,求P(![]() )的概率.
)的概率.
参考公式: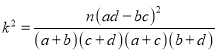 ,其中
,其中![]()
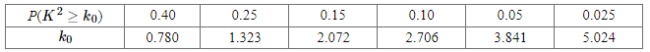
【答案】(1)没有超过![]() 的把握认为“停车是否超过6小时”与性别有关;(2)(i)分布列见解析,
的把握认为“停车是否超过6小时”与性别有关;(2)(i)分布列见解析,![]() ,(ii)
,(ii)![]()
【解析】
(1)用分层抽样的方法计算不超过6小时得车辆有40辆,结合![]() 列联表数据完善表格,并代入公式,计算出
列联表数据完善表格,并代入公式,计算出![]() 的值,与独立性检验判断表比较作出判断.
的值,与独立性检验判断表比较作出判断.
(2)(i)分析停车一次所交费用变量![]() 的可能值为5,8,11,15,19,30,并根据“以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率”求 出 对 应 概 率;列 出 分 布 列,求 期 望..
的可能值为5,8,11,15,19,30,并根据“以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率”求 出 对 应 概 率;列 出 分 布 列,求 期 望..
(2) (ii)服从二项分布,用二项分布的概率公式计算.
(1)![]() 列联表如下:
列联表如下:
男 | 女 | 合计 | |
不超过6小时 | 10 | 30 | 40 |
6小时以上 | 20 | 40 | 60 |
合计 | 30 | 70 | 100 |
根据上表数据代入公式可得![]()
所以没有超过![]() 的把握认为“停车是否超过6小时”与性别有关;
的把握认为“停车是否超过6小时”与性别有关;
(2)(i)由题意知,X的可能值为5,8,11,15,19,30,则
![]() ,
,![]() ,,
,,![]() ,
,
![]() ,
,![]()
所以X的分布列为
X | 5 | 8 | 11 | 15 | 19 | 30 |
|
|
|
|
|
|
|
![]()
(ii)由题意得![]()
所以![]()
所以![]() .
.

 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()