题目内容
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
,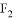 ,且
,且 ,点
,点 的椭圆上的点.
的椭圆上的点.
(1)求椭圆的 标准的方程;
标准的方程;
(2)若 为椭圆
为椭圆 上异于顶点的任意一点,
上异于顶点的任意一点, 、
、 分别是椭圆
分别是椭圆 的上顶点和右顶点,直线
的上顶点和右顶点,直线 交
交 轴于
轴于 ,直线
,直线 交
交 轴于
轴于 ,证明
,证明 为定值.
为定值.
练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
题目内容
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
,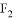 ,且
,且 ,点
,点 的椭圆上的点.
的椭圆上的点.
(1)求椭圆的 标准的方程;
标准的方程;
(2)若 为椭圆
为椭圆 上异于顶点的任意一点,
上异于顶点的任意一点, 、
、 分别是椭圆
分别是椭圆 的上顶点和右顶点,直线
的上顶点和右顶点,直线 交
交 轴于
轴于 ,直线
,直线 交
交 轴于
轴于 ,证明
,证明 为定值.
为定值.
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案