Question

【题目】已知椭圆C的中心在原点，焦点在x轴上，离心率为 ，短轴长为4 ． （Ⅰ）求椭圆C的标准方程；
（Ⅱ）直线x=2与椭圆C交于P、Q两点，A、B是椭圆O上位于直线PQ两侧的动点，且直线AB的斜率为 ．
①求四边形APBQ面积的最大值；
②设直线PA的斜率为k1 ， 直线PB的斜率为k2 ， 判断k1+k2的值是否为常数，并说明理由．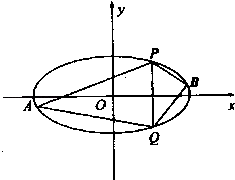

Answer 1

【答案】解：（Ⅰ）设椭圆C的方程为 ． 由已知b=2 ，离心率e= ，a2=b2+c2 ， 得a=4，
所以，椭圆C的方程为 ．
（Ⅱ）①由（Ⅰ）可求得点P、Q的坐标为P（2，3），Q（2，﹣3），则|PQ|=6，
设A（x1 ， y1），B（x2 ， y2），直线AB的方程为y= x+t，代入 ，
得：x2+tx+t2﹣12=0．
由△＞0，解得﹣4＜t＜4，由根与系数的关系得 ，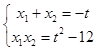
四边形APBQ的面积 ，
故当t=0时， ；
②由题意知，直线PA的斜率 ，直线PB的斜率 ，
则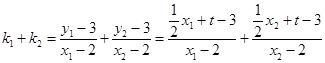
=
= ，
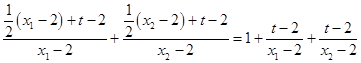
由①知 ，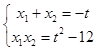
可得 ，
所以k1+k2的值为常数0
【解析】（Ⅰ）设椭圆C的方程为 ，由短轴长可得b值，根据离心率为 及a2=b2+c2 ， 得a值； （Ⅱ）①设A（x1 ， y1），B（x2 ， y2），直线AB的方程为y= x+t，代入 得x的二次方程，四边形APBQ的面积S= = ，而|PQ|易求，代入韦达定理即可求得S的表达式，由表达式即可求得S的最大值；②直线PA的斜率 ，直线PB的斜率 ，代入韦达定理即可求得k1+k2的值；
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：，焦点在y轴：才能正确解答此题．