题目内容
【题目】在数列{an},{bn}中,已知a1=2,b1=4,且﹣an , bn , an+1成等差数列,﹣bn , an , bn+1也成等差数列. (Ⅰ)求证:数列{an+bn}和{an﹣bn}都是等比数列,并求数列{an}的通项公式;
(Ⅱ)若cn=(an﹣3n)log3[an﹣(﹣1)n],求数列{cn}的前n项和Tn .
【答案】(I)证明:∵﹣an , bn , an+1成等差数列,﹣bn , an , bn+1也成等差数列. ∴bn= ![]() ,an=
,an= ![]() ,
,
∴an+bn= ![]() [(an+1+bn+1)﹣(an+bn)],即an+1+bn+1=3(an+bn),
[(an+1+bn+1)﹣(an+bn)],即an+1+bn+1=3(an+bn),
又∵a1+b1=1+2=3,∴数列{an+bn}是首项、公比均为3的等比数列;
同理可得:﹣an+bn= ![]() [(an+1﹣bn+1)+(﹣an+bn)],即an+1﹣bn+1=﹣(an﹣bn),
[(an+1﹣bn+1)+(﹣an+bn)],即an+1﹣bn+1=﹣(an﹣bn),
又∵﹣a1+b1=﹣1+2=1,
∴数列{bn﹣an}是首项为1、公比均为﹣1的等比数列,
∴bn﹣an=(﹣1)n+1 ,
又∵bn+an=3n ,
∴an= ![]() =
= ![]() [3n﹣(﹣1)n+1];
[3n﹣(﹣1)n+1];
(II)解:∵cn=(2an﹣3n)log3[2an﹣(﹣1)n]
=[3n﹣(﹣1)n+1﹣3n]log3[3n﹣(﹣1)n+1﹣(﹣1)n]
=(﹣1)nn,
∴Tn=﹣1+2﹣3+4﹣…+(﹣1)nn,
﹣Tn=1﹣2+3﹣4+…+(﹣1)n(n﹣1)+(﹣1)n+1n,
两式相减得:2Tn=﹣1+1﹣1+1﹣…﹣1﹣(﹣1)n+1n,
∴Tn= ![]() {
{ 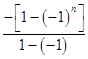 +(﹣1)nn}
+(﹣1)nn}
【解析】(I)﹣an , bn , an+1成等差数列,﹣bn , an , bn+1也成等差数列.可得bn= ![]() ,an=
,an= ![]() ,an+bn=
,an+bn= ![]() [(an+1+bn+1)﹣(an+bn)],即an+1+bn+1=3(an+bn),即可证明数列{an+bn}是首项、公比均为3的等比数列.同理可得:数列{bn﹣an}是首项为1、公比均为﹣1的等比数列.可得an=
[(an+1+bn+1)﹣(an+bn)],即an+1+bn+1=3(an+bn),即可证明数列{an+bn}是首项、公比均为3的等比数列.同理可得:数列{bn﹣an}是首项为1、公比均为﹣1的等比数列.可得an= ![]() .(II)cn=(2an﹣3n)log3[2an﹣(﹣1)n]=(﹣1)nn,利用“错位相减法”与等比数列的求和公式即可得出.
.(II)cn=(2an﹣3n)log3[2an﹣(﹣1)n]=(﹣1)nn,利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系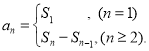 才能正确解答此题.
才能正确解答此题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案