题目内容
【题目】已知直线l：y=kx+b，(0<b<1)和圆O：
相交于A，B两点.
（1）当k=0时，过点A，B分别作圆O的两条切线，求两条切线的交点坐标；
（2）对于任意的实数k，在y轴上是否存在一点N，满足
？若存在，请求出此点坐标；若不存在，说明理由.
【答案】（1）
；（2）存在，.
【解析】
（1）求出交点
坐标，由过切点的半径与切线垂直得切线斜率从而得切线方程，两切线方程联立方程组可解得交点坐标；
（2）假设存在
满足题意，设
，由已知得
，
由直线方程与圆方程联立 消元后应用韦达定理得
，代入，由恒等式知识可得
．
（1）把
代入圆方程解得
，所以
，
圆
上过
点的切线为
，由
得
，
方程为
，化简得：
，
同理过
点的切线
方程是
，
两方程联立可得两直线交点坐标为
；
（2）假设
轴上存在点满足题意，设，
，
则
， 
，
，整理得
，①
由
得
，
，
，代入①式并整理得
，此式对任意实数
都成立，∴
．
故轴点的点
满足
．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
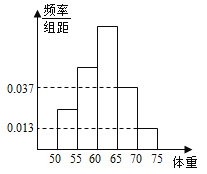
【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度，研究人员在某电影院随机抽取了1000名观众作调查，所得结果如下所示，其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
（Ⅰ）完善上述
列联表；
（Ⅱ）是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性？
附：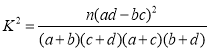
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
