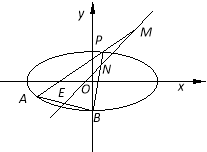
题目内容
【题目】(本题满分16分)如图,在平面直角坐标系![]() 中,离心率为
中,离心率为![]() 的椭圆
的椭圆![]()
![]() 的左顶点为
的左顶点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点.若直线
两点.若直线![]() 斜率为
斜率为![]() 时,
时, ![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试问以![]() 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线![]() 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
【答案】(1)![]() (2)过定点
(2)过定点![]() .
.
【解析】试题分析:(1)因为离心率为![]() ,所以要确定椭圆标准方程,只需再确定一个独立条件,即点P坐标:根据点
,所以要确定椭圆标准方程,只需再确定一个独立条件,即点P坐标:根据点![]() 斜率为
斜率为![]() 且
且![]() 可求
可求![]() ,所以
,所以![]() ,又
,又![]() ,解得椭圆
,解得椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)用点P坐标表示出![]() 的坐标及以
的坐标及以![]() 为直径的圆的方程:设
为直径的圆的方程:设![]() ,则直线
,则直线![]() 方程为:
方程为: ![]() ,∴
,∴ ,直线
,直线![]() 方程为:
方程为: ![]() ,∴
,∴ ,以
,以![]() 为直径的圆为
为直径的圆为 ,利用
,利用![]() 化简得
化简得![]() ,所以动圆必过
,所以动圆必过![]() 与
与![]() 的交点
的交点![]()
试题解析:解:(1)设 ,
,
∵直线![]() 斜率为
斜率为![]() 时,
时, ![]() ,∴
,∴ ,∴
,∴![]() 3分
3分
∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() . 6分
. 6分
(2)以![]() 为直径的圆过定点
为直径的圆过定点![]() .
.
设![]() ,则
,则![]() ,且
,且![]() ,即
,即![]() ,
,
∵![]() ,∴直线
,∴直线![]() 方程为:
方程为: ![]() ,∴
,∴ ,
,
直线![]() 方程为:
方程为: ![]() ,∴
,∴ , 9分
, 9分
以![]() 为直径的圆为
为直径的圆为
即![]() , 12分
, 12分
∵![]() ,∴
,∴![]() ,
,
令![]() ,
,![]() ,解得
,解得![]() ,
,
∴以![]() 为直径的圆过定点
为直径的圆过定点![]() . 16分
. 16分

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
【题目】(本小题满分为16分)设A,B分别为椭圆![]()
![]() 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为![]() ,且点
,且点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 与椭圆相交于异于
与椭圆相交于异于![]() 的点
的点![]() ,证明:△
,证明:△![]() 为钝角三角形.
为钝角三角形.
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |