题目内容
【题目】已知![]() (2,1),
(2,1),![]() (1,7),
(1,7),![]() (5,1),设C是直线OP上的一点(其中O为坐标原点)
(5,1),设C是直线OP上的一点(其中O为坐标原点)
(1)求使![]() 取到最小值时的
取到最小值时的![]() ;
;
(2)根据(1)中求出的点C,求cos∠ACB.
【答案】(1)![]() ;(2)cos∠ACB
;(2)cos∠ACB![]() .
.
【解析】
(1)根据题意设点![]() ,从而将
,从而将![]() 数量积的坐标表示求出来,可得一个关于x的二次函数,利用二次函数的性质,即可求得答案;
数量积的坐标表示求出来,可得一个关于x的二次函数,利用二次函数的性质,即可求得答案;
(2)根据(1)中的点C,可以求得![]() ,
,![]() 的坐标,利用向量的数量积即可求得cos∠ACB的值.
的坐标,利用向量的数量积即可求得cos∠ACB的值.
(1)∵![]() ,则直线OP的方程为y
,则直线OP的方程为y![]() ,
,
∵C是直线OP上的一点,则设点![]() ,
,
∴![]() ,
,
∴![]() (1﹣x)(5﹣x)+(7
(1﹣x)(5﹣x)+(7![]() )(1
)(1![]() )
)
![]()
![]() ,
,
∴当x=4时,![]() 取到最小值,此时C(4,2),
取到最小值,此时C(4,2),
∴![]() ;
;
(2)由(1)可知,C(4,2),
∴![]() ,
,
∴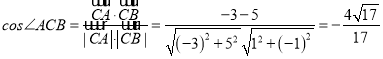 ,
,
故cos∠ACB![]() .
.

练习册系列答案
相关题目