题目内容
已知函数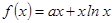 的图象在点
的图象在点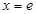 (e为自然对数的底数)处取得极值-1.
(e为自然对数的底数)处取得极值-1.
(1)求实数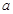 的值;
的值;
(2)若不等式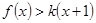 对任意
对任意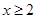 恒成立,求
恒成立,求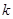 的取值范围.
的取值范围.
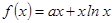 的图象在点
的图象在点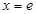 (e为自然对数的底数)处取得极值-1.
(e为自然对数的底数)处取得极值-1.(1)求实数
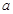 的值;
的值;(2)若不等式
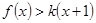 对任意
对任意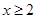 恒成立,求
恒成立,求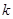 的取值范围.
的取值范围.(1)-2;(2)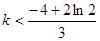
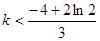
试题分析:(1)因为函数
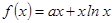 的图象在点
的图象在点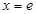 (e为自然对数的底数)处取得极值-1,所以
(e为自然对数的底数)处取得极值-1,所以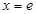 时导函数的值为零.即可求出
时导函数的值为零.即可求出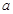 的值.
的值.(2)因为不等式
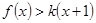 对任意
对任意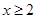 恒成立,所以写出等价的不等式,从而转化为求函数的在
恒成立,所以写出等价的不等式,从而转化为求函数的在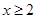 时的最小值的问题.所以通过对函数的求导,观察发现函数的单调性即可得到函数的在
时的最小值的问题.所以通过对函数的求导,观察发现函数的单调性即可得到函数的在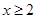 范围的最小值.从而得到结论.
范围的最小值.从而得到结论.试题解析:(1)解:因为
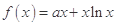 ,所以
,所以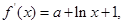
因为函数
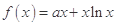 的图像在点
的图像在点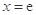 处取得极值,
处取得极值,所以
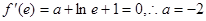 . 4分
. 4分(2)解:由(1)知,
 ,
,所以
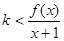 对任意
对任意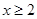 恒成立,即
恒成立,即 对任意
对任意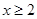 恒成立.
恒成立.令
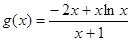 ,则,
,则,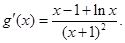
因为
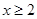 ,所以
,所以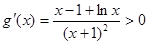 ,
,所以函数
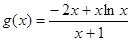 在
在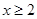 上为增函数,
上为增函数,则
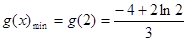 ,
,所以
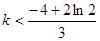 . 12分
. 12分
练习册系列答案
相关题目
 (件)与销售单价
(件)与销售单价 (元/件)可近似看作一次函数
(元/件)可近似看作一次函数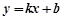 的关系(如图所示).
的关系(如图所示). 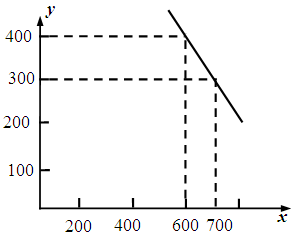
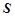 元. 试用销售单价
元. 试用销售单价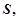 并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?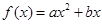
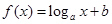

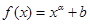
 及点
及点 ,在
,在 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 .设
.设 所表示图形的面积为________.
所表示图形的面积为________.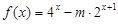 ,若存在实数
,若存在实数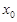 ,使得
,使得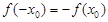 成立,则实数
成立,则实数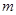 的取值范围是( ) w
的取值范围是( ) w


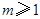
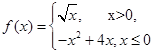 ,若
,若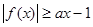 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )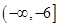
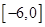
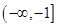
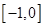
 ,则函数
,则函数 的值域为
的值域为



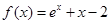 的零点所在的区间为
的零点所在的区间为