题目内容
已知圆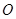 :
: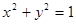 ,点
,点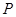 在直线
在直线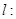
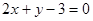 上,过点
上,过点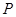 作圆
作圆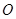 的两条切线,
的两条切线,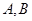 为两切点,
为两切点,
(1)求切线长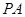 的最小值,并求此时点
的最小值,并求此时点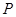 的坐标;
的坐标;
(2)点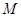 为直线
为直线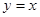 与直线
与直线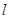 的交点,若在平面内存在定点
的交点,若在平面内存在定点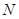 (不同于点
(不同于点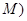 ,满足:对于圆
,满足:对于圆 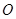 上任意一点
上任意一点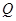 ,都有
,都有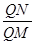 为一常数,求所有满足条件的点
为一常数,求所有满足条件的点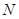 的坐标;
的坐标;
(3)求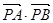 的最小值.
的最小值.
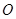 :
: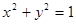 ,点
,点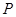 在直线
在直线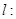
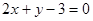 上,过点
上,过点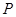 作圆
作圆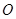 的两条切线,
的两条切线,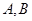 为两切点,
为两切点,(1)求切线长
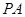 的最小值,并求此时点
的最小值,并求此时点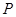 的坐标;
的坐标;(2)点
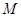 为直线
为直线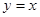 与直线
与直线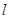 的交点,若在平面内存在定点
的交点,若在平面内存在定点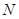 (不同于点
(不同于点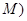 ,满足:对于圆
,满足:对于圆 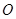 上任意一点
上任意一点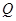 ,都有
,都有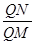 为一常数,求所有满足条件的点
为一常数,求所有满足条件的点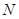 的坐标;
的坐标;(3)求
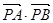 的最小值.
的最小值.解(1)设点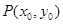
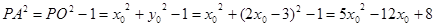
=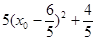
故当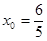 ,即
,即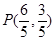 时,
时,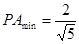 ………………………………5分
………………………………5分
(2)由题: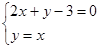 ,
,
设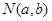 ,
,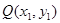 ,满足
,满足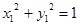
则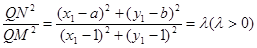
整理得: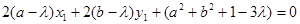 ,对任意的点
,对任意的点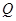 都成立,可得
都成立,可得
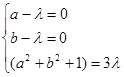 解得
解得 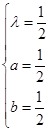 ,或
,或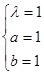 (舍)
(舍)

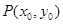
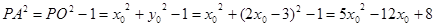
=
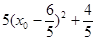
故当
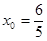 ,即
,即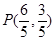 时,
时,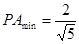 ………………………………5分
………………………………5分(2)由题:
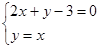 ,
,
设
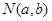 ,
,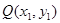 ,满足
,满足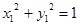
则
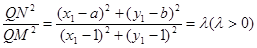
整理得:
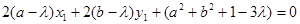 ,对任意的点
,对任意的点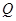 都成立,可得
都成立,可得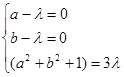 解得
解得 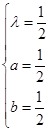 ,或
,或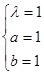 (舍)
(舍)
略

练习册系列答案
相关题目
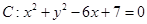 的切线,切点为A,则切线PA的长为 。
的切线,切点为A,则切线PA的长为 。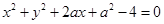 与
与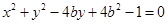 恰有三条公切
恰有三条公切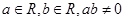 ,则
,则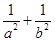 的最小值为( )
的最小值为( )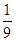
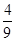
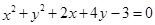 上,且到直线
上,且到直线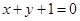 的距离为
的距离为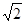 的点共有( )
的点共有( )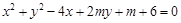 与
与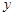 轴的两交点
轴的两交点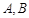 位于原点的同侧,则实数
位于原点的同侧,则实数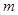

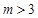 或
或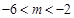
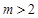 或
或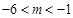
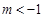
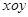 中,已知“葫芦”曲线
中,已知“葫芦”曲线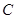 由圆弧
由圆弧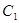 与圆弧
与圆弧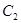 相接而成,两相接点
相接而成,两相接点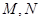 均在直线
均在直线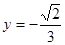 上.圆弧
上.圆弧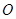 ,半径为
,半径为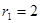 ;圆弧
;圆弧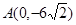 .
.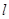 :
: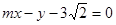 与“葫芦”曲线
与“葫芦”曲线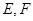 两点.当
两点.当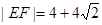 时,求直线
时,求直线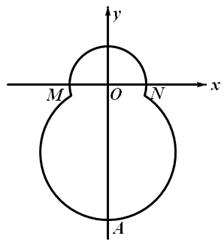
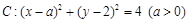 及直线
及直线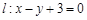 . 当直线
. 当直线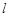 被圆
被圆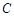 截得的弦长为
截得的弦长为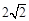 时,
时,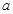 的值;
的值; 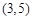 并与圆
并与圆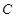 经过两点
经过两点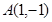 和
和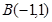 ,且圆心在直线
,且圆心在直线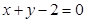 上。
上。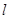 与圆
与圆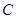 相交于点
相交于点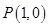 和点
和点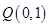 。
。