题目内容
在边长为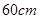 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?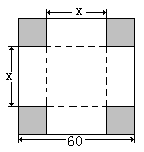
当箱底边长为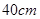 时,箱子容积最大,最大容积是
时,箱子容积最大,最大容积是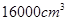 .
.
解析试题分析:设箱底边长为
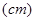 ,则无盖的方底箱子的高
,则无盖的方底箱子的高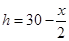
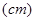 ,其体积为
,其体积为 ,从而可得
,从而可得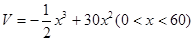 ,通过求导,讨论导数的正负得函数的增减性,根据函数的单调性可求体积的最大值.
,通过求导,讨论导数的正负得函数的增减性,根据函数的单调性可求体积的最大值.
试题解析:设箱底边长为
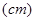 ,则无盖的方底箱子的高
,则无盖的方底箱子的高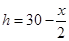
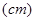 ,其体积为
,其体积为
则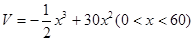
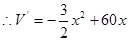
令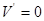 ,得
,得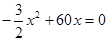 ,解得
,解得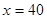 (
(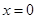 舍去)
舍去)
当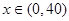 时,
时,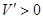 ;当
;当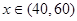 时,
时,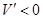
所以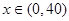 时,
时,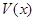 单调递增;
单调递增;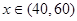 时,
时,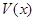 单调递减,所以函数
单调递减,所以函数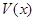 在
在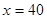 时取得极大值, 结合实际情况,这个极大值就是函数
时取得极大值, 结合实际情况,这个极大值就是函数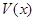 的最大值.
的最大值. 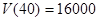
故当箱底边长为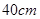 时,箱子容积最大,最大容积是
时,箱子容积最大,最大容积是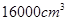 .
.
考点:导数在实际中的运用.

练习册系列答案
相关题目
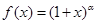 的定义域是
的定义域是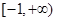 ,其中常数
,其中常数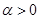 .
.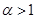 ,求
,求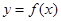 的过原点的切线方程.
的过原点的切线方程.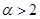 时,求最大实数
时,求最大实数 ,使不等式
,使不等式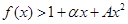 对
对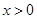 恒成立.
恒成立.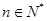 ,有
,有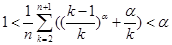 .
.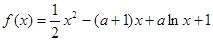
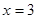 是
是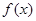 的极值点,求
的极值点,求 的范围,使得
的范围,使得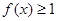 恒成立.
恒成立.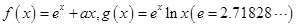 ..
..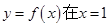 处的切线为
处的切线为 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为 ,求a的值;
,求a的值;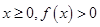 恒成立,试确定
恒成立,试确定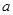 的取值范围;
的取值范围;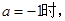 是否存在实数
是否存在实数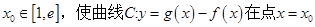 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出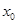 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.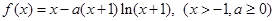 .
. 的单调区间;
的单调区间;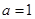 时,若方程
时,若方程 在
在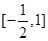 上有两个实数解,求实数
上有两个实数解,求实数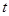 的取值范围;
的取值范围; 时,
时,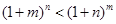 .
.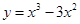 .
.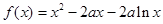 ,
,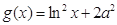 ,其中
,其中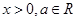 .
.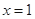 是函数
是函数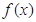 的极值点,求
的极值点,求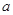 的值;
的值;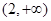 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;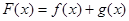 ,求证:
,求证: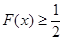 .
.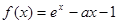
 的单调增区间
的单调增区间 内单调递增,求
内单调递增,求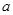 的取值范围.
的取值范围. .
.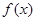 的最大值;
的最大值;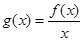 ,证明:
,证明: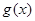 有最大值
有最大值 ,且
,且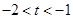 .
.