题目内容
已知函数f(x)=x2,g(x)=2elnx(x>0)(e为自然对数的底数).
(1)求F(x)=f(x)-g(x)(x>0)的单调区间及最小值;
(2)是否存在一次函数y=kx+b(k,b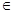 R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.
R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.
(1)当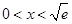 时,F(x)在
时,F(x)在 上单调递减;当
上单调递减;当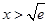 时,F(x)在
时,F(x)在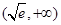 上单调递增.
上单调递增.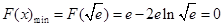 ;(2)存在一次函数
;(2)存在一次函数 ,使得当x>0时,
,使得当x>0时,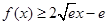 ,且
,且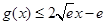 恒成立.
恒成立.
解析试题分析:本题主要考查导数的运算、利用导数研究函数的单调性及最值等数学知识,考查学生的分析问题解决问题的能力和计算能力.第一问,对 求导,利用
求导,利用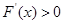 ,
, 解出单调区间,通过单调性判断出最小值所在位置,并且求出即可;第二问,通过第一问的求解可以知道
解出单调区间,通过单调性判断出最小值所在位置,并且求出即可;第二问,通过第一问的求解可以知道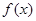 与
与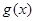 图像有且仅有一个公共点,猜想所求的直线就是在公共点处的公切线,下面只需对猜想进行证明即可,只需证明当x>0时,
图像有且仅有一个公共点,猜想所求的直线就是在公共点处的公切线,下面只需对猜想进行证明即可,只需证明当x>0时,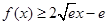 ,且
,且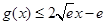 恒成立即可,进一步转化为证明
恒成立即可,进一步转化为证明 ,
, 即可,通过构造函数,利用导数求最值进行证明.
即可,通过构造函数,利用导数求最值进行证明.
试题解析:(1)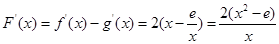 (x>0),
(x>0),
令F′(x)=0,得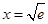 (
(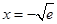 舍),
舍),
∴当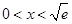 时,F′(x)<0,F(x)在
时,F′(x)<0,F(x)在 上单调递减;
上单调递减;
当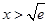 时,F′(x)>0,F(x)在
时,F′(x)>0,F(x)在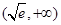 上单调递增.
上单调递增.
∴当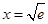 时,F(x)有极小值,也是最小值,
时,F(x)有极小值,也是最小值,
即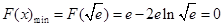 .
.
∴F(x)的单调递增区间为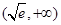 ,单调递减区间为
,单调递减区间为 ,最小值为0.(7分)
,最小值为0.(7分)
(2)由(1)知,f(x)与g(x)的图象有且仅有一个公共点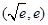 ,
,
∴猜想:一次函数的图象就是f(x)与g(x)的图象在点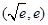 处的公切线,
处的公切线,
其方程为 .
.
下面证明:当x>0时,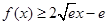 ,且
,且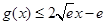 恒成立.
恒成立.
∵ ,∴
,∴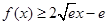 对x>0恒成立.
对x>0恒成立.
又令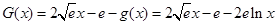 ,∴
,∴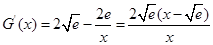 ,
,
∴当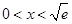 时,
时,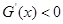 ,G(x)在
,G(x)在 上单调递减;
上单调递减;
当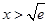 时,G′(x)>0,G(x)在
时,G′(x)>0,G(x)在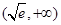 上单调递增.
上单调递增.
∴当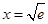 时,G(x)有极小值,也是最小值,
时,G(x)有极小值,也是最小值,
即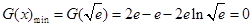 ,∴G(x)≥0,即
,∴G(x)≥0,即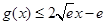 恒成立.
恒成立.
故存在一次函数 ,使得当x>0时,
,使得当x>0时,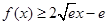 ,且
,且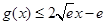 恒成立.(14分)
恒成立.(14分)
考点:1.利用导数判断函数的单调性;2.利用导数求函数的最值.

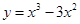 .
. 为实数,函数
为实数,函数 .
. 的单调区间与极值;
的单调区间与极值;  且
且 时,
时, .
.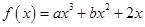 在
在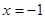 处取得极值,且在点
处取得极值,且在点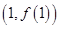 处的切线斜率为
处的切线斜率为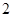 .
.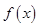 的单调增区间;
的单调增区间; 的方程
的方程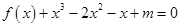 在区间
在区间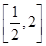 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数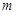 的取值范围.
的取值范围. .
.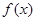 的最大值;
的最大值;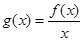 ,证明:
,证明: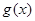 有最大值
有最大值 ,且
,且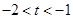 .
.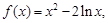
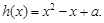
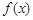 的极值;
的极值;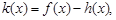 若函数
若函数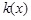 在
在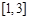 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数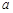 的取值范围.
的取值范围.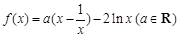 .
.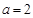 ,求曲线
,求曲线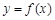 在点
在点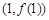 处的切线方程;
处的切线方程;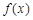 的单调区间;
的单调区间;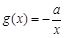 .若至少存在一个
.若至少存在一个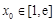 ,使得
,使得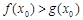 成立,求实数
成立,求实数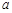 的取值范围.
的取值范围.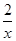 -3ln x,其中a为常数.
-3ln x,其中a为常数.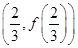 处的切线的斜率为1时,求函数f(x)在
处的切线的斜率为1时,求函数f(x)在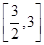 上的最小值;
上的最小值;