题目内容
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形 (如图所示,其中O为圆心,
(如图所示,其中O为圆心,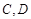 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).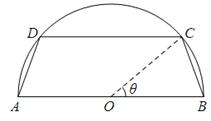
(1)求V关于θ的函数表达式;
(2)求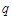 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
(1)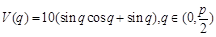 ;(2)
;(2)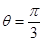 ;(3)是.
;(3)是.
解析试题分析:(1)本题求直四棱柱的体积,关键是求底面面积,我们要用底面半径1和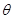 表示出等腰梯形的上底
表示出等腰梯形的上底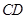 和高,从图形中可知高为
和高,从图形中可知高为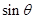 ,而
,而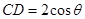 ,因此面积易求,体积也可得出;(2)我们在(1)中求出
,因此面积易求,体积也可得出;(2)我们在(1)中求出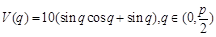 ,这里
,这里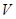 的最大值可利用导数知识求解,求出
的最大值可利用导数知识求解,求出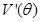 ,解出方程
,解出方程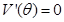 在
在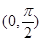 上的解,然后考察在解
上的解,然后考察在解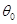 的两边
的两边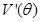 的正负性,确定
的正负性,确定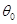 是最大值点,实质上对应用题来讲,导数值为0的那个唯一点就是要求的极值点);(3),上(2)我们可能把木梁的表面积用
是最大值点,实质上对应用题来讲,导数值为0的那个唯一点就是要求的极值点);(3),上(2)我们可能把木梁的表面积用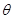 表示出来,
表示出来,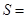
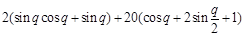
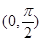 ,由于
,由于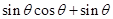 在体积
在体积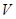 中出现,因此我们可求
中出现,因此我们可求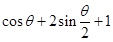 的最大值,这里可不用导数来求,因为
的最大值,这里可不用导数来求,因为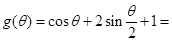
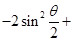
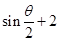 ,可借助二次函数知识求得最大值,如果这里
,可借助二次函数知识求得最大值,如果这里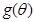 取最大值时的
取最大值时的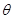 和
和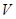 取最大值的
取最大值的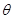 取值相同,则结论就是肯定的.
取值相同,则结论就是肯定的.
试题解析:(1)梯形 的面积
的面积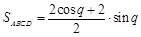 =
=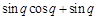 ,
,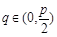 . 2分
. 2分
体积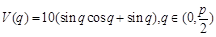 . 3分
. 3分
(2)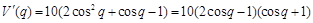 .
.
令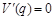 ,得
,得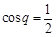 ,或
,或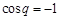 (舍).
(舍).
∵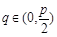 ,∴
,∴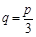 . 5分
. 5分
当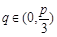 时,
时,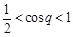 ,
,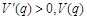 为增函数;
为增函数;
当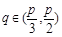 时,
时,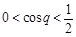 ,
,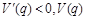 为减函数. 7分
为减函数. 7分
∴当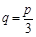 时,体积V最大. 8分
时,体积V最大. 8分
(3)木梁的侧面积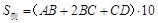 =
=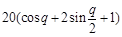 ,
,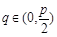 .
.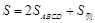 =
=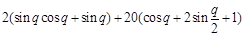 ,
,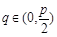 . 10分
. 10分
设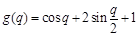 ,
,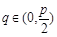 .∵
.∵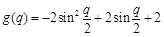 ,
,
∴当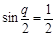 ,即
,即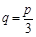 时,
时,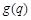 最大. 12分
最大. 12分
又由(2)知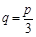 时,
时,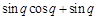 取得最大值,
取得最大值,
所以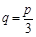 时,木梁的表面积S最大. 13分
时,木梁的表面积S最大. 13分
综上,当木梁的体积V最大时,其表面积S也最大. 14分
考点:(1)函数解析式;(2)用导数求最值;(3)四棱柱的表面积及其最值.

练习册系列答案
相关题目
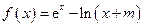 .
.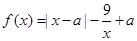 ,
,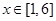 ,
,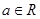 .
.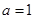 ,试判断并用定义证明函数
,试判断并用定义证明函数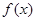 的单调性;
的单调性;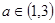 时,求函数
时,求函数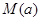 .
.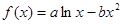 图像上一点
图像上一点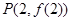 处的切线方程为
处的切线方程为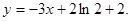 (1)求
(1)求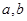 的值;(2)若方程
的值;(2)若方程 在区间
在区间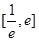 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令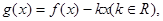 如果
如果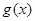 的图像与
的图像与 轴交于
轴交于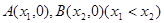 两点,
两点,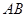 的中点为
的中点为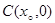 ,求证:
,求证: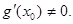
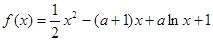
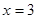 是
是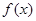 的极值点,求
的极值点,求 的范围,使得
的范围,使得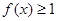 恒成立.
恒成立.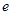 是自然对数的底数,函数
是自然对数的底数,函数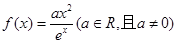 .
. 的单调递增区间;
的单调递增区间;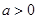 时,函数
时,函数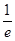 ,求
,求 的值.
的值.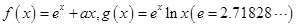 ..
..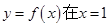 处的切线为
处的切线为 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为 ,求a的值;
,求a的值;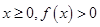 恒成立,试确定
恒成立,试确定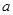 的取值范围;
的取值范围;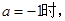 是否存在实数
是否存在实数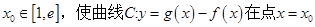 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出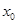 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.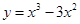 .
.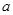 为实数,函数
为实数,函数 .
. 的单调区间与极值;
的单调区间与极值;  且
且 时,
时, .
.