题目内容
已知函数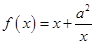 ,
,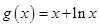 ,其中
,其中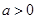 .
.
(1)若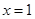 是函数
是函数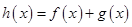 的极值点,求实数
的极值点,求实数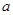 的值;
的值;
(2)若对任意的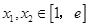 (
(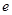 为自然对数的底数)都有
为自然对数的底数)都有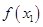 ≥
≥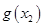 成立,求实数
成立,求实数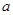 的取值范围.
的取值范围.
(1)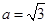 (2)
(2)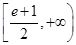
解析试题分析:(1)先求导,根据题意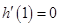 (2)可将问题转化为
(2)可将问题转化为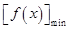 ≥
≥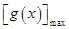 ,分别求导令导数大于0、小于0得单调性,用单调性求最值。在解导数大于0或小于0的过程中注意对
,分别求导令导数大于0、小于0得单调性,用单调性求最值。在解导数大于0或小于0的过程中注意对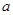 的讨论。
的讨论。
试题解析:(1)解法1:∵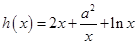 ,其定义域为
,其定义域为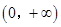 ,
,
∴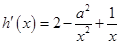 . ∵
. ∵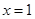 是函数
是函数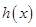 的极值点,∴
的极值点,∴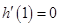 ,即
,即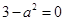 .
.
∵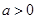 ,∴
,∴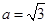 . 经检验当
. 经检验当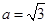 时,
时,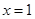 是函数
是函数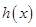 的极值点,∴
的极值点,∴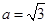 .、
.、
解法2:∵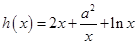 ,其定义域为
,其定义域为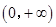 ,
,
∴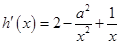 . 令
. 令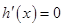 ,即
,即 ,整理,得
,整理,得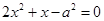 .
.
∵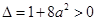 ,
,
∴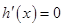 的两个实根
的两个实根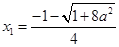 (舍去),
(舍去),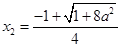 ,
,
当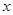 变化时,
变化时,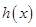 ,
,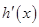 的变化情况如下表:
的变化情况如下表: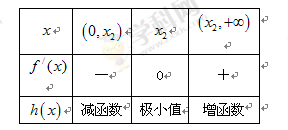
依题意,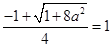 ,即
,即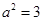 ,∵
,∵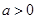 ,∴
,∴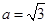 .
.
(2)对任意的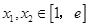 都有
都有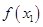 ≥
≥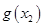 成立等价于对任意的
成立等价于对任意的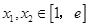 都有
都有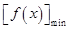 ≥
≥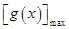 .当
.当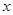
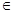 [1,
[1,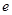 ]时,
]时, .
.
∴函数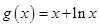 在
在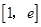 上是增函数.∴
上是增函数.∴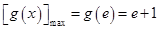 .
.
∵ ,且
,且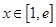 ,
,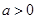 .
.
①当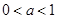 且
且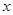
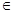 [1,
[1,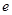 ]时,
]时,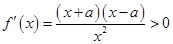 ,
,
∴函数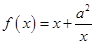 在[1,
在[1,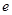 ]上是增函数,
]上是增函数,
∴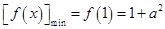 .由
.由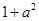 ≥
≥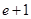 ,得
,得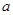 ≥
≥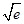 ,又
,又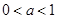 ,∴
,∴

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
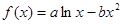 图像上一点
图像上一点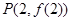 处的切线方程为
处的切线方程为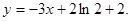 (1)求
(1)求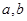 的值;(2)若方程
的值;(2)若方程 在区间
在区间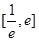 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令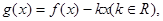 如果
如果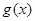 的图像与
的图像与 轴交于
轴交于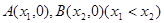 两点,
两点,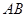 的中点为
的中点为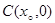 ,求证:
,求证: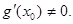
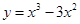 .
.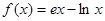 ,
, 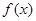 的单调区间;
的单调区间;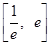 内存在
内存在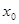 ,使不等式
,使不等式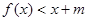 成立,求
成立,求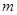 的取值范围.
的取值范围.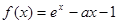
 的单调增区间
的单调增区间 内单调递增,求
内单调递增,求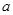 的取值范围.
的取值范围. (如图所示,其中O为圆心,
(如图所示,其中O为圆心,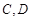 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).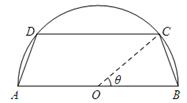
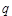 的值,使体积V最大;
的值,使体积V最大; .
. 的单调区间与极值;
的单调区间与极值;  且
且 时,
时, .
.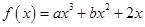 在
在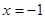 处取得极值,且在点
处取得极值,且在点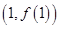 处的切线斜率为
处的切线斜率为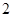 .
.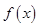 的单调增区间;
的单调增区间; 的方程
的方程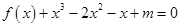 在区间
在区间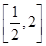 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数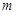 的取值范围.
的取值范围.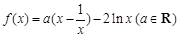 .
.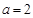 ,求曲线
,求曲线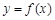 在点
在点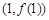 处的切线方程;
处的切线方程;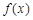 的单调区间;
的单调区间;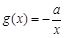 .若至少存在一个
.若至少存在一个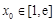 ,使得
,使得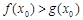 成立,求实数
成立,求实数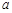 的取值范围.
的取值范围.