题目内容
定义域是一切实数的函数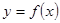 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
(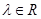 )
)
使得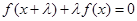 对任意实数
对任意实数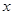 都成立,则称
都成立,则称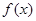 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
①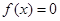 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“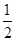 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③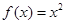 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
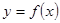 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
(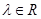 )
)使得
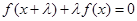 对任意实数
对任意实数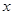 都成立,则称
都成立,则称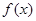 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有下列关于“
 —伴随函数”的结论:
—伴随函数”的结论:①
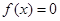 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;②“
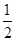 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;③
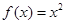 是一个“
是一个“ —伴随函数”;
—伴随函数”;其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
A
试题分析:①不正确,原因如下.
若f(x)=c≠0,则取λ=-1,则f(x-1)-f(x)=c-c=0,既f(x)=c≠0是-1-伴随函数
,②不正确,原因如下.
若 f(x)=x2是一个λ-伴随函数,则(x+λ)2+λx2=0.推出λ=0,λ=-1,矛盾
③正确.若f(x)是
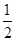 -伴随函数.
-伴随函数.则f(x+
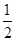 )+
)+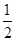 f(x)=0,
f(x)=0,取x=0,则f(
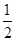 )+
)+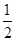 f(0)=0,若f(0),f(
f(0)=0,若f(0),f(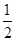 )任一个为0,函数f(x)有零点.
)任一个为0,函数f(x)有零点.若f(0),f(
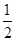 )均不为零,则f(0),f(
)均不为零,则f(0),f(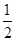 )异号,由零点存在定理,在(0,
)异号,由零点存在定理,在(0,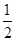 )
)区间存在x0,
f(x0)=0.即
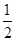 -伴随函数至少有一个零点.
-伴随函数至少有一个零点.故选A。
点评:新定义问题,正确理解f(x)是λ-伴随函数的定义,是解答本题的关键.

练习册系列答案
相关题目
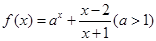 .
.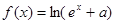 (
(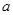 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数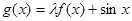 是区间[-1,1]上的减函数
是区间[-1,1]上的减函数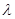 的取值范围;
的取值范围; 在
在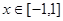 上恒成立,求
上恒成立,求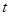 的取值范围。
的取值范围。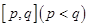 ,使得函数在区间
,使得函数在区间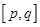 上的值域为
上的值域为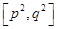 .
.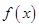 的图像经过点
的图像经过点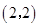 ,判断
,判断
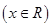 是否是和谐函数?
是否是和谐函数? 是否是和谐函数?
是否是和谐函数? 是和谐函数,求实数
是和谐函数,求实数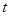 的取值范围.
的取值范围.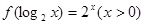 ,则
,则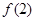 的值是( )
的值是( )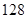
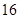
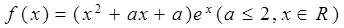
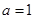 ,求函数
,求函数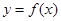 在点(0,
在点(0,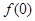 )处的切线方程;
)处的切线方程;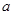 ,使得
,使得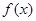 的极大值为3.若存在,求出
的极大值为3.若存在,求出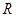 的函数
的函数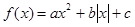
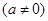 有四个单调区间,则实数
有四个单调区间,则实数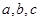 满足( )
满足( )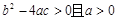
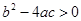
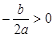
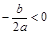
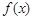 的定义域为
的定义域为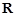 ,
,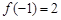 ,对任意
,对任意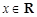 ,
,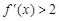 ,则
,则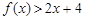 的解集为:
的解集为: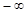 ,+
,+ )
)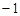 ,1)
,1)