题目内容
【题目】已知椭圆![]() +y2=1上两个不同的点A,B关于直线y=mx+
+y2=1上两个不同的点A,B关于直线y=mx+![]() 对称.
对称.
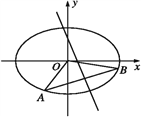
(1)求实数m的取值范围;
(2)求△AOB面积的最大值(O为坐标原点).
【答案】(1)m<-![]() 或m>
或m>![]() .(2)
.(2)![]()
【解析】试题分析:(1)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程消去
,代入椭圆方程消去![]() ,设
,设![]() ,可得
,可得![]() ,设线段
,设线段![]() 的中点
的中点![]() ,利用中点坐标公式及其根与系数的可得
,利用中点坐标公式及其根与系数的可得![]() ,代入直线
,代入直线![]() ,可得
,可得![]() ,代入
,代入![]() ,即可解出
,即可解出![]() 的范围;(2)结合(1),
的范围;(2)结合(1),![]() 换元后根据韦达定理、弦长公式、点到直线距离公式,利用三角形面积公式,将三角形面积用
换元后根据韦达定理、弦长公式、点到直线距离公式,利用三角形面积公式,将三角形面积用![]() 表示,再利用二次函数配方法即可得出三角形面积的最大值.
表示,再利用二次函数配方法即可得出三角形面积的最大值.
试题解析: (1) 由题意知m≠0,
可设直线AB的方程为y=-![]() x+b.
x+b.
由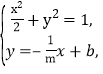 消去y,得
消去y,得![]() +
+![]() x2-
x2-![]() x+b2-1=0.
x+b2-1=0.
因为直线y=-![]() x+b与椭圆
x+b与椭圆![]() +y2=1有两个不同的交点, 所以Δ=-2b2+2+
+y2=1有两个不同的交点, 所以Δ=-2b2+2+![]() >0,①
>0,①
将线段AB中点M(![]() ,
,![]() )代入直线方程y=mx+
)代入直线方程y=mx+![]() ,解得b=-
,解得b=-![]() .②
.②
由①②得m<-![]() 或m>
或m>![]() .
.
(2)令t=![]() ∈(-
∈(-![]() ,0)∪(0,
,0)∪(0,![]() ),
),
则|AB|=![]() ·
·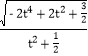 ,
,
且O到直线AB的距离为d=![]() .
.
设△AOB的面积为S(t),
所以S(t)=![]() |AB|·d=
|AB|·d=![]() ≤
≤![]() .
.
当且仅当t2=![]() 时,等号成立.
时,等号成立.
故△AOB面积的最大值为![]() .
.
【方法点晴】本题主要考查直线与椭圆的位置关系及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用配方法法求三角形面积最值的.

练习册系列答案
相关题目