Question

【题目】已知函数的图象在处的切线为.（为自然对数的底数）.

（1）求，的值；

（2）当时，求证：；

（3）若对任意的恒成立，求实数的取值范围.

Answer 1

【答案】（1）（2）见解析（3）

【解析】

（1）因为，可得，根据函数的图象在处的切线为，即可求得答案；

（2）由（1）可知，.令，，由，得，当时，，单调递减；当时，，单调递增，即可求得答案；

（3）因为对任意的恒成立，可得 对任意的恒成立，令，，结合已知，即可求得答案.

（1），

.

函数的图象在处的切线为

.

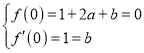解得：

（2）由（1）可知，.

令，，由，得，

当时，，单调递减；

当时，，单调递增.

，

.

（3）对任意的恒成立

对任意的恒成立，

令，，

.

由（2）可知当时，恒成立，

令，得；

，得.

的增区间为，减区间为

故.

，

实数的取值范围为.