题目内容
12.计算:(0.0064)${\;}^{-\frac{1}{4}}$-($\frac{7}{8}$)0+[($\sqrt{2}$)3]${\;}^{-\frac{4}{3}}$+16-0.75.分析 化小数为分数,化根式为分数指数幂,然后利用有理指数幂的运算性质化简求值.
解答 解:(0.0064)${\;}^{-\frac{1}{4}}$-($\frac{7}{8}$)0+[($\sqrt{2}$)3]${\;}^{-\frac{4}{3}}$+16-0.75
=$[(\frac{2\sqrt{2}}{10})^{4}]^{-\frac{1}{4}}-1+(\sqrt{2})^{-4}$$+({2}^{4})^{-\frac{3}{4}}$
=$(\frac{\sqrt{2}}{5})^{-1}-1+{2}^{-2}+{2}^{-3}$
=$\frac{5\sqrt{2}}{2}-1+\frac{1}{4}+\frac{1}{8}$
=$\frac{5\sqrt{2}}{2}-\frac{5}{8}$.
点评 本题考查有理指数幂的化简与求值,考查了有理指数幂的运算性质,是基础的计算题.

练习册系列答案
相关题目
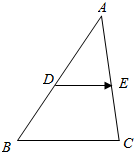 如图所示,在△ABC中,已知D为AB的中点,E为AC的中点,试判断$\overrightarrow{DE}$与$\overrightarrow{BC}$是否共线.
如图所示,在△ABC中,已知D为AB的中点,E为AC的中点,试判断$\overrightarrow{DE}$与$\overrightarrow{BC}$是否共线.