题目内容
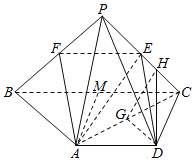
【题目】在四棱锥P﹣ABCD中,![]() ,E是PC的中点,平面PAC⊥平面ABCD.
,E是PC的中点,平面PAC⊥平面ABCD.

(1)证明:ED∥平面PAB;
(2)若![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取PB的中点F,连接AF,EF,通过证明四边形ADEF是平行四边形,得到DE∥AF,从而证出ED∥平面PAB;
(2)通过做辅助线找到二面角A﹣PC﹣D的平面角,求出其余弦值即可.
(1)证明:取PB的中点F,连接AF,EF.
∵EF是△PBC的中位线,∴EF∥BC,且EF![]() .
.
又AD=BC,且AD![]() BC,∴AD∥EF且AD=EF,
BC,∴AD∥EF且AD=EF,
∴四边形ADEF是平行四边形.∴DE∥AF,
又DE面ABP,AF面ABP,
∴ED∥面PAB.
(2)解:取BC的中点M,连接AM,则AD∥MC且AD=MC,
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上.
∴AB⊥AC,可得AC![]() .
.
过D作DG⊥AC于G,
∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,
∴DG⊥平面PAC,则DG⊥PC.
过G作GH⊥PC于H,则PC⊥面GHD,连接DH,则PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.
在△ADC中,GD![]() ,
,
连接AE, cos∠ACE![]() ,
,
AE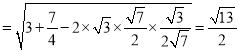 ,
,
∵点P到AC的距离d1![]() ,
,
∴点A到PC的距离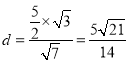 .
.
GH![]() .
.
在Rt△GDH中,HD![]() ,
,
∴cos∠GHD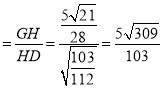 .
.
即二面角A﹣PC﹣D的余弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

