题目内容
6.求适合下列条件的圆锥曲线的标准方程:(1)焦点在直线x-2y+4=0上,且开口向上的抛物线;
(2)与双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1有公共的渐近线,且过点(3$\sqrt{2}$,0)的双曲线.
分析 (1)由题意,焦点在y轴上,分别求出焦点坐标,然后根据抛物线的标准形式可得答案.
(2)设出双曲线方程,利用双曲线上的点,求解即可.
解答 解:(1)由题意,焦点在y轴上,根据x=0,x-2y+4=0可得焦点坐标为(0,2),
∴抛物线的标准方程为x2=8y;
(2)与双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1有公共的渐近线,
可设双曲线方程为:$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=k,
双曲线经过点(3$\sqrt{2}$,0),∴k=2,
∴双曲线的方程为$\frac{{x}^{2}}{18}-\frac{{y}^{2}}{32}$=1.
点评 本题主要考查抛物线、双曲线的标准方程.属基础题.

练习册系列答案
相关题目
18.已知f(x)=ax3+bx+1(ab≠0),若f(2015)=k,则f(-2015)=( )
| A. | k-2 | B. | 2-k | C. | 1-k | D. | -k-1 |
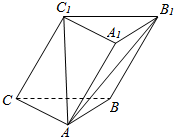 如图,三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC.
如图,三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC.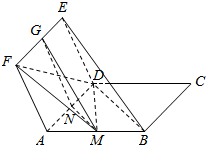 如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.