题目内容
14.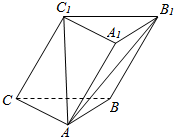 如图,三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC.
如图,三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC.(1)求证:AC1⊥BC;
(2)求BA1与AC1所成的角;
(3)求CB1与平面AC1B1所成角的正弦值;
(4)求二面角C-AC1-B1的余弦值;
(5)若AB=2,求A1到平面AB1C1的距离.
分析 (1)建立坐标系,证明$\overrightarrow{A{C}_{1}}$•$\overrightarrow{BC}$=0,可得AC1⊥BC;
(2)利用$\overrightarrow{A{C}_{1}}$•$\overrightarrow{B{A}_{1}}$=0求BA1与AC1所成的角;
(3)求出平面AC1B1的法向量,求CB1与平面AC1B1所成角的正弦值;
(4)求出平面CAC1的法向量,即可求二面角C-AC1-B1的余弦值;
(5)若AB=2,平面AC1B1的法向量为$\overrightarrow{n}$=(1,0,1),$\overrightarrow{A{A}_{1}}$=(0,1,$\sqrt{3}$),即可求A1到平面AB1C1的距离.
解答 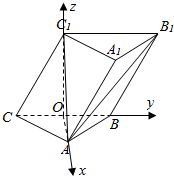 (1)证明:∵三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC,∴取BC的中点O,则OC1⊥平面ABC,OA⊥BC.
(1)证明:∵三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC,∴取BC的中点O,则OC1⊥平面ABC,OA⊥BC.
建立如图所示的坐标系,设底面边长2,则A($\sqrt{3}$,0,0),C1(0,0,$\sqrt{3}$),B(0,1,0),C(0,-1,0),∴$\overrightarrow{A{C}_{1}}$=(-$\sqrt{3}$,0,$\sqrt{3}$),$\overrightarrow{BC}$=(0,-2,0),
∴$\overrightarrow{A{C}_{1}}$•$\overrightarrow{BC}$=0,
∴AC1⊥BC;
(2)解:A1($\sqrt{3}$,1,$\sqrt{3}$),∴$\overrightarrow{B{A}_{1}}$=($\sqrt{3}$,0,$\sqrt{3}$),
∴$\overrightarrow{A{C}_{1}}$•$\overrightarrow{B{A}_{1}}$=0,
∴BA1与AC1所成的角为90°;
(3)解:∵B1(0,2,$\sqrt{3}$),∴$\overrightarrow{A{B}_{1}}$=(-$\sqrt{3}$,2,$\sqrt{3}$),$\overrightarrow{C{B}_{1}}$=(0,3,$\sqrt{3}$)
设平面AC1B1的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{-\sqrt{3}x+2y+\sqrt{3}z=0}\\{-\sqrt{3}x+\sqrt{3}z=0}\end{array}\right.$,∴$\overrightarrow{n}$=(1,0,1)
∴CB1与平面AC1B1所成角的正弦值为$\frac{\sqrt{3}}{\sqrt{9+3}•\sqrt{2}}$=$\frac{\sqrt{2}}{4}$;
(4)同理可得平面CAC1的法向量为(1,-$\sqrt{3}$,1)
∴二面角C-AC1-B1的余弦值为$\frac{2}{\sqrt{2}•\sqrt{5}}$=$\frac{\sqrt{10}}{5}$;
(5)解:AB=2,平面AC1B1的法向量为$\overrightarrow{n}$=(1,0,1),$\overrightarrow{A{A}_{1}}$=(0,1,$\sqrt{3}$),
∴A1到平面AB1C1的距离$\frac{\sqrt{3}}{\sqrt{2}}$=$\frac{\sqrt{6}}{2}$.
点评 本题考查知识点,考查空间向量的运用,正确建立坐标系,求平面的法向量是关键.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | t | 4.8 | 6.7 |
| A. | 4.7 | B. | 4.6 | C. | 4.5 | D. | 4.4 |
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,0]∪[1,2] | D. | [1,2] |
①$\sqrt{2}$∈R;②0∈N*;③{-2}⊆Z,④∅={0}.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |