题目内容
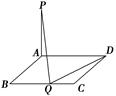
[2012·辽宁高考]已知正三棱锥P-ABC,点P,A,B,C都在半径为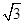 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
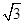 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.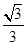
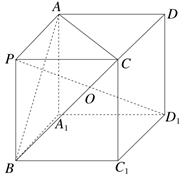
依题意,以PA,PB,PC为棱构造如图所示的正方体,且此球为正方体的外接球,PD1为球的直径,PD1的中点O为球心,由PD1=2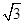 ,可得PA=PB=PC=2,由等积法可得三棱锥P-ABC的高为
,可得PA=PB=PC=2,由等积法可得三棱锥P-ABC的高为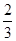
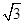 ,∴球心O到平面ABC的距离为
,∴球心O到平面ABC的距离为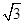 -
-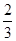
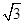 =
=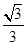 .
.
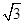 ,可得PA=PB=PC=2,由等积法可得三棱锥P-ABC的高为
,可得PA=PB=PC=2,由等积法可得三棱锥P-ABC的高为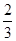
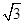 ,∴球心O到平面ABC的距离为
,∴球心O到平面ABC的距离为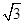 -
-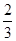
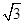 =
=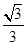 .
.

练习册系列答案
相关题目
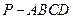 中,底面
中,底面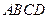 为平行四边形,
为平行四边形,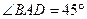 ,
,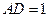 ,
,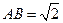 ,
,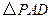 是正三角形,平面
是正三角形,平面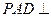 平面
平面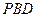 .
.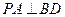 ;
; 的体积.
的体积.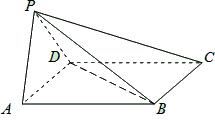
 中,
中, ,
,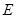 为
为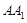 的中点,
的中点,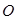 为
为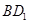 的中点.
的中点.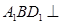 平面
平面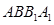 ;
;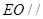 平面
平面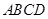 ;
;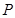 为正方体
为正方体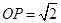 的点
的点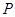 的个数,并说明理由.
的个数,并说明理由.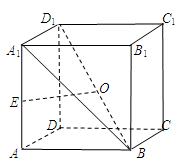
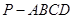 中,底面
中,底面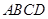 是平行四边形,
是平行四边形,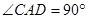 ,
,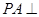 平面
平面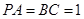 ,
,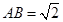 ,
,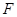 是
是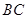 的中点.
的中点.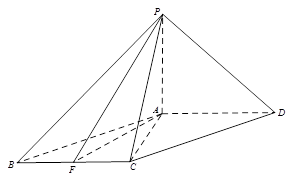
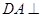 平面
平面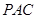 ;
; 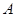 为坐标原点,射线
为坐标原点,射线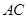 、
、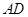 、
、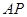 分别是
分别是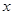 轴、
轴、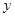 轴、
轴、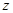 轴的正半轴,建立空间直角坐标系,已经计算得
轴的正半轴,建立空间直角坐标系,已经计算得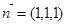 是平面
是平面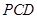 的法向量,求平面
的法向量,求平面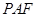 与平面
与平面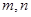 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给定下列四个命题:
是两个不重合的平面,给定下列四个命题: ,
,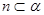 ,则
,则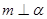 ;
;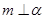 ,
,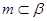 ,则
,则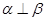 ;
; ,则
,则 ;
;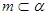 ,
, ,
, ,则
,则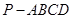 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为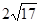 .点
.点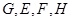 分别是棱
分别是棱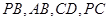 上共面的四点,平面
上共面的四点,平面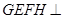 平面
平面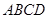 ,
,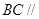 平面
平面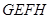 .
.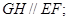
 ,求四边形
,求四边形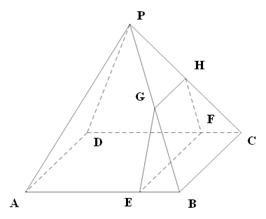
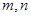 是两条不同直线,
是两条不同直线, 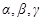 是三个不同平面,则下列正确的是( )
是三个不同平面,则下列正确的是( ) ,则
,则
 ,则
,则
 ,则
,则 ,则
,则