题目内容
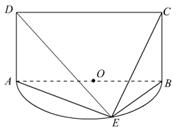
如图,在四棱锥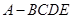 中,平面
中,平面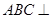 平面
平面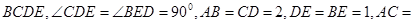
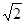 .
.
(1)证明: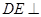 平面
平面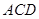 ;
;
(2)求二面角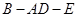 的大小
的大小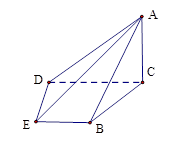
(1)详见解析;(2)二面角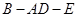 的大小是
的大小是 .
.
解析试题分析:(1)求证: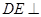 平面
平面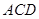 ,证明线面垂直,先证线线垂直,即证线和平面内两条相交直线垂直,由已知可得
,证明线面垂直,先证线线垂直,即证线和平面内两条相交直线垂直,由已知可得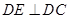 ,只需证明
,只需证明 ,或
,或 ,由已知平面
,由已知平面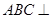 平面
平面 ,只需证明
,只需证明 ,就得
,就得 平面
平面 ,即
,即 ,而由已知
,而由已知 ,在直角梯形
,在直角梯形 中,易求
中,易求 ,从而满足
,从而满足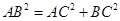 ,即得
,即得 ,问题得证;(2)求二面角
,问题得证;(2)求二面角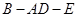 的大小,可用传统方法,也可用向量法,用传统方法,关键是找二面角的平面角,可利用三垂线定理来找,但本题不存在利用三垂线定理的条件,因此利用垂面法,即作
的大小,可用传统方法,也可用向量法,用传统方法,关键是找二面角的平面角,可利用三垂线定理来找,但本题不存在利用三垂线定理的条件,因此利用垂面法,即作 ,与
,与 交于点
交于点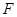 ,过点
,过点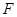 作
作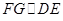 ,与
,与 交于点
交于点 ,连结
,连结 ,由(1)知,
,由(1)知, ,则
,则 ,,所以
,,所以 是二面角
是二面角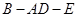 的平面角,求出
的平面角,求出 的三条边,利用余弦定理,即可求出二面角
的三条边,利用余弦定理,即可求出二面角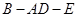 的大小,用向量法,首先建立空间坐标系,先找三条两两垂直的直线作为坐标轴,观察几何图形可知,以
的大小,用向量法,首先建立空间坐标系,先找三条两两垂直的直线作为坐标轴,观察几何图形可知,以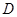 为原点,分别以射线
为原点,分别以射线 为
为 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系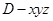 ,写出个点坐标,设出设平面
,写出个点坐标,设出设平面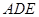 的法向量为
的法向量为 ,平面
,平面 的法向量为
的法向量为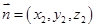 ,求出它们的一个法向量,利用法向量的夹角与二面角的关系,即可求出二面角
,求出它们的一个法向量,利用法向量的夹角与二面角的关系,即可求出二面角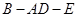 的大小.
的大小.
(1)在直角梯形 中,由
中,由 ,
, 得,
得, ,由
,由 ,则
,则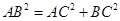 ,即
,即 ,又平面
,又平面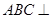 平面
平面 ,从而
,从而 平面
平面 ,所以
,所以 ,又
,又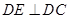 ,从而
,从而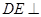 平面
平面 ;
;
(2)方法一:作 ,与
,与 交于点
交于点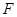 ,过点
,过点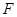 作
作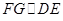 ,与
,与 交于点
交于点 ,连结
,连结 ,由(1)知,
,由(1)知, ,则
,则 ,,所以
,,所以 是二面角
是二面角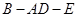 的平面角,在直角梯形
的平面角,在直角梯形 中,由
中,由 ,得
,得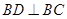 ,又平面
,又平面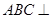 平面
平面

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 与点
与点 ,则线段
,则线段 之间的距离是
之间的距离是 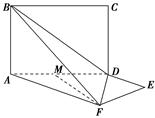
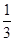 ,求AB的长.
,求AB的长. 中,
中, 分别是棱
分别是棱 的中点,点
的中点,点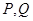 分别在棱
分别在棱 ,
,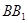 上移动,且
上移动,且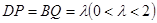 .
. 时,证明:直线
时,证明:直线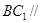 平面
平面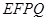 ;
; ,使平面
,使平面 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出
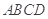 是正方形,
是正方形,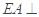 平面
平面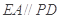 ,
,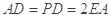 ,
,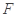 ,
,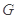 ,
, 分别为
分别为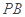 ,
,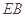 ,
,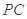 的中点.
的中点.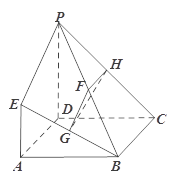
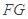
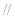 平面
平面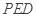 ;
;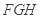 与平面
与平面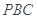 所成锐二面角的大小.
所成锐二面角的大小. 中,底面
中,底面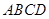 是直角梯形,
是直角梯形, ,
, ,
,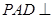 平面
平面
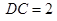 ,
,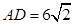 ,
, ,
, ,且
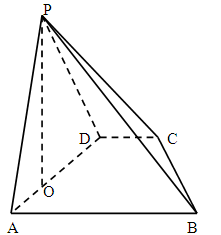
,且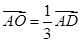 .
.
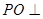 平面
平面 与平面
与平面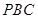 所成二面角的大小为
所成二面角的大小为 ,求
,求 的值.
的值.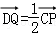 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.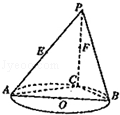
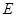 是以
是以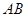 为直径的半圆
为直径的半圆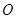 上异于
上异于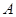 、
、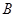 的点,矩形
的点,矩形 所在的平面垂直于半圆
所在的平面垂直于半圆 .
.
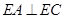 ;
;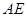 和
和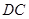 所成的角为
所成的角为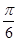 ,求平面
,求平面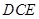 与平面
与平面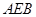 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.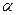 ,且l的方向向量为(2, m, 1), 平面
,且l的方向向量为(2, m, 1), 平面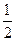 , 2), 则m= .
, 2), 则m= .