题目内容
如图,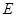 是以
是以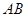 为直径的半圆
为直径的半圆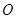 上异于
上异于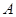 、
、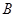 的点,矩形
的点,矩形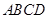 所在的平面垂直于半圆
所在的平面垂直于半圆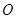 所在的平面,且
所在的平面,且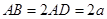 .
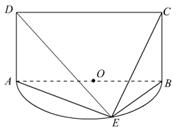
.
(1)求证: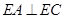 ;
;
(2)若异面直线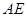 和
和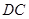 所成的角为
所成的角为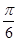 ,求平面
,求平面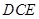 与平面
与平面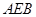 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(1)证明过程详见解析;(2)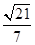 .
.
解析试题分析:本题主要考查线线垂直、线面垂直、面面垂直、二面角、向量法等基础知识,考查学生的空间想象能力、逻辑推理能力和计算能力.第一问,先利用面面垂直的性质得到线面垂直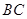 垂直于圆
垂直于圆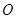 所在的平面,再利用线面垂直的性质得到
所在的平面,再利用线面垂直的性质得到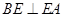 ,而在圆内AB为直径,所以
,而在圆内AB为直径,所以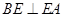 ,利用线面垂直的判定得
,利用线面垂直的判定得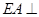 平面
平面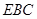 ,最后利用线面垂直的性质得到结论
,最后利用线面垂直的性质得到结论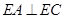 ;第二问,利用向量法,先根据已知条件中的垂直关系建立空间直角坐标系,得到有关点及向量的坐标,利用向量法中的公式,求出平面DCE和平面AEB的法向量,再利用夹角公式求夹角的余弦值.
;第二问,利用向量法,先根据已知条件中的垂直关系建立空间直角坐标系,得到有关点及向量的坐标,利用向量法中的公式,求出平面DCE和平面AEB的法向量,再利用夹角公式求夹角的余弦值.
试题解析:(1)∵平面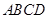 垂直于圆
垂直于圆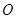 所在的平面,两平面的交线为
所在的平面,两平面的交线为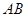 ,
,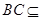 平面
平面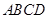 ,
,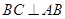 ,∴
,∴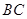 垂直于圆
垂直于圆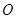 所在的平面.又
所在的平面.又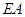 在圆
在圆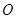 所在的平面内,∴
所在的平面内,∴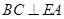 .∵
.∵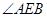 是直角,∴
是直角,∴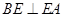 ,∴
,∴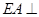 平面
平面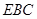 ,∴
,∴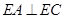 . 6分
. 6分
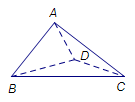
(2)如图,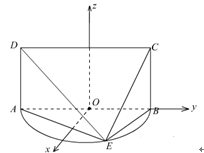
以点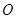 为坐标原点,
为坐标原点,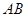 所在的直线为
所在的直线为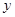 轴,过点
轴,过点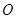 与
与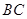 平行的直线为
平行的直线为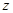 轴,建立空间直角坐标系
轴,建立空间直角坐标系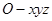 .由异面直线
.由异面直线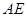 和
和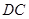 所成的角为
所成的角为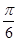 ,
,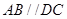 知
知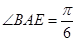 ,
,
∴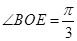 ,∴
,∴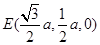 ,由题设可知
,由题设可知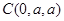 ,
,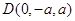 ,∴
,∴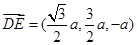 ,
,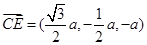 .设平面
.设平面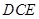 的一个法向量为
的一个法向量为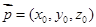 ,
,
由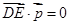 ,
,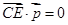 得
得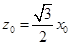 ,
,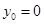 ,取
,取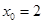 ,得
,得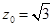 .
.
∴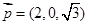 .又平面
.又平面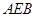 的一个法向量为
的一个法向量为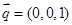 ,∴
,∴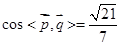 .
.
平面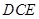 与平面
与平面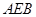 所成的锐二面角的余弦值
所成的锐二面角的余弦值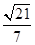 . 13分
. 13分
(其他解法可参考给分)
考点:线线垂直、线面垂直、面面垂直、二面角、向量法.

练习册系列答案
相关题目
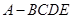 中,平面
中,平面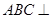 平面
平面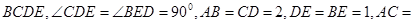
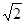 .
.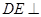 平面
平面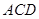 ;
;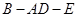 的大小
的大小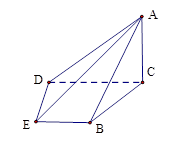
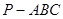 中,直线
中,直线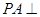 平面
平面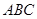 ,且
,且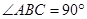 ,又点
,又点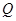 ,
,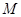 ,
,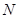 分别是线段
分别是线段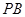 ,
,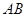 ,
,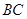 的中点,且点
的中点,且点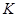 是线段
是线段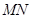 上的动点.
上的动点.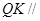 平面
平面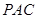 ;
;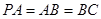 ,求二面角
,求二面角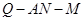 的平面角的余弦值.
的平面角的余弦值.
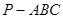 中,直线
中,直线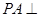 平面
平面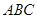 ,且
,且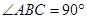 ,又点
,又点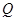 ,
, ,
,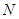 分别是线段
分别是线段 ,
,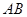 ,
,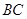 的中点,且点
的中点,且点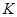 是线段
是线段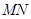 上的动点.
上的动点.
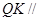 平面
平面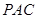 ;
;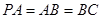 ,求二面角
,求二面角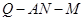 的平面角的余弦值.
的平面角的余弦值.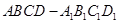 中,底面
中,底面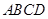 和侧面
和侧面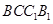 都
都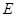 是
是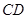 的中点,
的中点,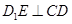 ,
,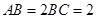 .
.
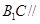 平面
平面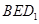 ;
;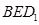 所成的锐二面角的大小为
所成的锐二面角的大小为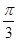 ,求线段
,求线段 的长度.
的长度.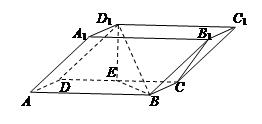

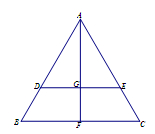
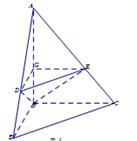
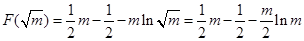 沿AF折起,得到如图所示的三棱锥
沿AF折起,得到如图所示的三棱锥 ,其中
,其中 .
.
 //平面
//平面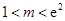 ;
;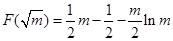 ;
;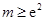 时,求三棱锥
时,求三棱锥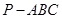 中,
中,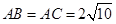 ,
,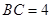 ,
, ,点
,点 在平面
在平面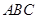 内的射影恰为
内的射影恰为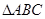 的重心
的重心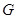 ,M为侧棱
,M为侧棱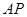 上一动点.
上一动点.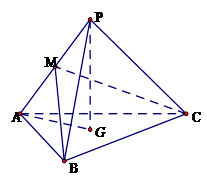
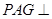 平面
平面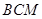 ;
;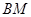 与平面
与平面 所成角的正弦值.
所成角的正弦值.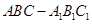 中,O是AC的中点,
中,O是AC的中点,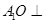 平面
平面 ,
,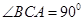 ,
,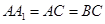 .
.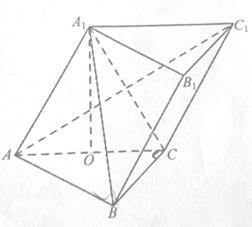
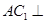 平面
平面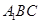 ;
; 的余弦值.
的余弦值.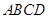 中,
中,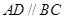 ,
,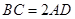
 ,
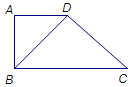
,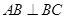 ,如图,把
,如图,把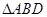 沿
沿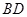 翻折,使得平面
翻折,使得平面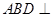 平面
平面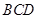 .
.
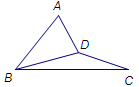
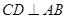 ;
;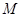 为线段
为线段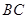 中点,求点
中点,求点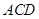 的距离;
的距离;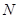 ,使得
,使得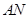 与平面
与平面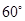 ?若存在,求出
?若存在,求出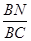 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.