题目内容
13.二次函数f(x)=2x2-mx+5,对任意x都有f(2+x)=f(4-x),则m=12.分析 由题设函数f(x)对任意x都有f(2+x)=f(4-x),故其对称轴为x=3,利用二次函数f(x)=2x2-mx+5,即可求出m.
解答 解:由题设函数f(x)对任意x都有f(2+x)=f(4-x),故其对称轴为x=3,
∵二次函数f(x)=2x2-mx+5,
∴$\frac{m}{4}$=3,
∴m=12.
故答案为:12.
点评 本题考查二次函数的对称性,考查学生的计算能力,确定函数的对称轴是关键.

练习册系列答案
相关题目
3.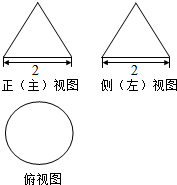 已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为( )
已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为( )
 已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为( )
已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为( )| A. | $\frac{4}{3}$π | B. | $\frac{8}{3}$π | C. | $\frac{16}{3}$π | D. | $\frac{32}{3}$π |
1.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量X与Y,且X,Y的分布列为
(1)求a,b的值;
(2)计算X,Y的期望与方差,并以此分析甲、乙技术状况.
| X | 1 | 2 | 3 |
| P | a | 0.1 | 0.6 |
| Y | 1 | 2 | 3 |
| P | 0.3 | b | 0.3 |
(2)计算X,Y的期望与方差,并以此分析甲、乙技术状况.
8.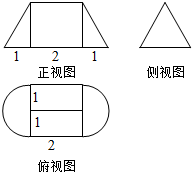 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | 2$\sqrt{3}$+$\frac{{\sqrt{3}π}}{3}$ | D. | 2$\sqrt{3}$+$\sqrt{3}$π |
18.如图是高尔顿板的改造装置,当小球从B自由下落时,进入槽口A处的概率为( )


| A. | $\frac{3}{16}$ | B. | $\frac{5}{16}$ | C. | $\frac{3}{32}$ | D. | $\frac{5}{32}$ |
