题目内容
若存在区间M=[a,b](a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间”.给出下列四个函数:①y=ex,x∈R;②f(x)=x3;③f(x)=cos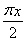 ;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).
;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).
②③
【解析】根据新定义逐一判断.因为函数y=ex,x∈R递增,且ex>x,x∈R恒成立,函数y=ex,x∈R不存在“稳定区间”,故①不存在“稳定区间”;函数f(x)=x3存在稳定区间[-1,0]或[0,1]或[-1,1],故②存在“稳定区间”;函数f(x)=cos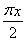 存在稳定区间[0,1],故③存在“稳定区间”;函数
存在稳定区间[0,1],故③存在“稳定区间”;函数
f(x)=ln x+1在(0,+∞)上递增,且ln x+1≤x,x>0恒成立,函数f(x)=ln x+1在定义域上不存在“稳定区间”,故④不存在“稳定区间”.

练习册系列答案
相关题目