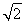Question

已知曲线y＝(a－3)x3＋ln x存在垂直于y轴的切线，函数f(x)＝x3－ax2－3x＋1在[1,2]上单调递增，则a的取值范围为________．

 

Answer 1

(－∞，0]

【解析】由已知条件可得方程y′＝3(a－3)x2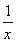＋＝0(x＞0)，即3(a－3)x3＋1＝0有大于0的实数根，即得x3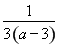＝－＞0，解得a＜3，又由函数f(x)＝x3－ax2－3x＋1在[1,2]上单调递增，可得不等式f′(x)＝3x2－2ax－3≥0在[1,2]上恒成立，即得a≤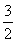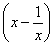在[1,2]上恒成立，由函数y＝x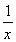－在[1,2]上单调递增可得，该函数的最小值为0，∴a≤0，综上可得实数a的取值范围为(－∞，0]．