题目内容
已知定义域为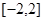 的函数
的函数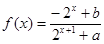 是奇函数.
是奇函数.
(Ⅰ)求实数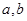 的值; (Ⅱ)解关于
的值; (Ⅱ)解关于 的不等式
的不等式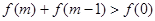 .
.
(Ⅰ)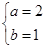 .(Ⅱ)原不等式的解集为
.(Ⅱ)原不等式的解集为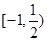 .
.
解析试题分析:(Ⅰ)由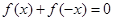 得:
得: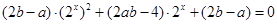 ,
,
所以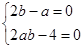 ,
,
解得: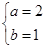 或
或 (舍去),
(舍去),
因此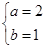 .
.
(Ⅱ)∵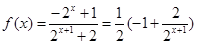 ,
,
∴函数 在
在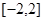 上单调递减,
上单调递减,
由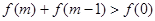 得:
得: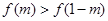 ,
,
所以 ,
,
解得: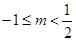 ,
,
所以原不等式的解集为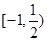 .
.
考点:本题主要考查函数的奇偶性及单调性的应用。
点评:中档题,研究函数的奇偶性,要注意定义域关于原点对称,其次,研究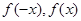 的关系。抽象不等式,往往要利用奇偶性、单调性转化成具体不等式求解。
的关系。抽象不等式,往往要利用奇偶性、单调性转化成具体不等式求解。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
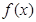 在
在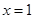 处取得极大值,求函数
处取得极大值,求函数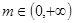 ,不等式
,不等式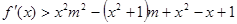 恒成立,求
恒成立,求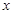 的取值范围
的取值范围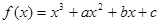 的图象过点
的图象过点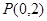 ,且点
,且点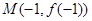 处的切线方程为在
处的切线方程为在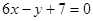 .
.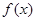 的解析式; (2)求函数
的解析式; (2)求函数 上的两个函数
上的两个函数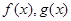 ,若存在一次函数
,若存在一次函数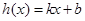 使得,对任意的
使得,对任意的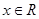 ,都有
,都有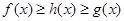 ,则把函数
,则把函数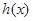 的图像叫函数
的图像叫函数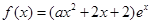 (
(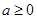 ,
,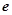 为自然对数的底数),
为自然对数的底数),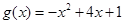
 的递增区间;
的递增区间;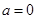 时,函数
时,函数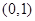 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数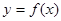 在
在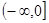 上递增,函数f(x)的一个零点为
上递增,函数f(x)的一个零点为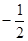 ,
,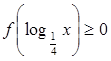 的x的取值集合.
的x的取值集合.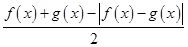 的最大值;
的最大值;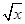 )>kg(x)对x∈[2,4]有解,求实数k的取值范围.
)>kg(x)对x∈[2,4]有解,求实数k的取值范围.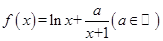
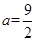 时,如果函数
时,如果函数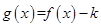 仅有一个零点,求实数
仅有一个零点,求实数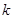 的取值范围.
的取值范围.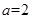 时,比较
时,比较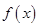 与1的大小.
与1的大小.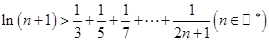
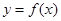 是定义在
是定义在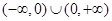 上的奇函数,当
上的奇函数,当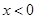 时,
时,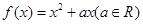 ,且
,且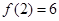 。
。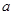 的值,(2)求
的值,(2)求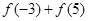 的值.
的值.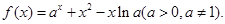
 在点
在点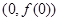 处的切线方程;
处的切线方程;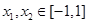 ,使得
,使得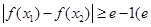 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围.