题目内容
【题目】已知函数
.
（1）若
对
恒成立，求
的取值范围；
（2）证明：不等式
对于正整数
恒成立，其中
为自然对数的底数.
【答案】（1）
（2）见解析
【解析】试题分析：（1）第（1）问，方法一，构造函数
，再分析f(x)的最大值和零的关系得到a的取值范围.方法二，分离参数得到
恒成立，即a大于F(x)的最大值. (2)第（2）问，先要把证明的不等式转化，再由第（1）问，
恒成立，得到
恒成立，把数列的通项放缩，对数列求和，再化简证明不等式.
试题解析：
（1）法一：记，
则
，
，
①当
时，
∵
，∴
，∴
在
上单减，
又
，∴
，即
在上单减，
此时，
，即
,所以a≥1.
②当
时，
考虑
时，
，∴在
上单增，
又
，∴
，即在上单増，
,不满足题意.
综上所述，.
法二：当时，
等价于，
，记
，则
，
∴
在上单减，∴
，
∴
，即
在上单减，
，故.
（2）由（1）知：取
，当
时，恒成立，
即恒成立，即恒成立，
即
对于恒成立，
由此，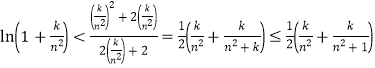
，
，
于是
，
故
.
练习册系列答案
名校课堂系列答案
相关题目
