题目内容
15.设F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,椭圆C上的一点P(x0,x0)(x0>0)到y轴的距离等于$\frac{\sqrt{5}}{5}$a.(1)求椭圆C的离心率;
(2)点F2关于直线OP的对称点为H,直线HF1交椭圆C于Q,K两点,当△F2QK的面积等于$\frac{4\sqrt{6}}{5}$时,求椭圆C的方程.
分析 (1)求得P($\frac{\sqrt{5}}{5}$a,$\frac{\sqrt{5}}{5}$a),代入椭圆方程,由a,b,c的关系和离心率公式,计算即可得到离心率;
(2)可设b=t,a=2t,c=$\sqrt{3}$t,则F2($\sqrt{3}$t,0),直线OP的方程为y=x,求得H的坐标,直线HF1的方程,代入椭圆方程,运用韦达定理,由三角形的面积公式,计算即可得到所求方程.
解答 解:(1)由题意可得x0=$\frac{\sqrt{5}}{5}$a,
由P($\frac{\sqrt{5}}{5}$a,$\frac{\sqrt{5}}{5}$a)在椭圆上,可得
$\frac{1}{5}$+$\frac{{a}^{2}}{5{b}^{2}}$=1,即有a=2b,
c=$\sqrt{{a}^{2}-{b}^{2}}$=$\frac{\sqrt{3}}{2}$a,
则椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$;
(2)可设b=t,a=2t,c=$\sqrt{3}$t,
则F2($\sqrt{3}$t,0),直线OP的方程为y=x,
即有H(0,$\sqrt{3}$t),F1(-$\sqrt{3}$t,0),
直线HF1的方程为y=x+$\sqrt{3}$t,
椭圆的方程为$\frac{{x}^{2}}{4{t}^{2}}$+$\frac{{y}^{2}}{{t}^{2}}$=1,
联立直线方程和椭圆方程,可得
5y2-2$\sqrt{3}$ty-t2=0,
可得y1+y2=$\frac{2\sqrt{3}}{5}$t,y1y2=-$\frac{{t}^{2}}{5}$,
|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{\frac{12{t}^{2}}{25}+\frac{4{t}^{2}}{5}}$=$\frac{4\sqrt{2}t}{5}$,
即有△F2QK的面积为S=${S}_{△Q{F}_{1}{F}_{2}}$+${S}_{△K{F}_{1}{F}_{2}}$
=$\frac{1}{2}$•2$\sqrt{3}t$•|y1-y2|=$\sqrt{3}$t•$\frac{4\sqrt{2}t}{5}$=$\frac{4\sqrt{6}}{5}$t2=$\frac{4\sqrt{6}}{5}$,
解得t=1,即有a=2,b=1,
则椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1.
点评 本题考查椭圆的方程和性质,考查离心率的求法,直线方程和椭圆方程联立,运用韦达定理,考查三角形的面积的求法,属于中档题.

 小题狂做系列答案
小题狂做系列答案| 工作代码 | 紧前工作 | 紧后工作 | 工期/时 |
| A | C | G | 2 |
| B | D | 无 | 3 |
| C | 无 | A、D、F | 4 |
| D | C | B | 2 |
| E | F | 无 | 4 |
| F | C | E | 2 |
| G | A | 无 | 5 |
 如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).
如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).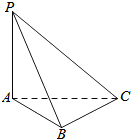 如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.
如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.