题目内容
8.已知函数$f(x)=3sin({ωx+\frac{π}{3}})\;({ω>0})$和g(x)=2cos(2x+φ)+1$({|φ|<\frac{π}{2}})$的图象的对称轴完全相同则φ的值为( )| A. | $\frac{π}{6}$ | B. | $-\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $-\frac{π}{3}$ |
分析 由条件利用正弦函数的周期性,求得ω=2,再利用正弦函数和余弦函数的图象的对称性,求得φ的值.
解答 解:由题意可得,这两个函数的周期相同,故有$\frac{2π}{ω}$=$\frac{2π}{2}$,求得ω=2.
对于f(x)=3sin(2x+$\frac{π}{3}$),令2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,可得 x=$\frac{kπ}{2}$+$\frac{π}{12}$,k∈Z,
故函数f(x)图象的对称轴方程为 x=$\frac{kπ}{2}$+$\frac{π}{12}$,k∈Z.
对于g(x)=2cos(2x+φ)+1,令2x+φ=kπ,可得 x=$\frac{kπ}{2}$-$\frac{φ}{2}$,k∈Z,
故-$\frac{φ}{2}$=$\frac{π}{12}$,∴φ=-$\frac{π}{6}$,
故选:B.
点评 本题主要考查正弦函数的周期性,正弦函数和余弦函数的图象的对称性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.设直线l1、l2的方向向量分别为$\overrightarrow a$=(2,-2,-2),$\overrightarrow b$=(2,0,4),则直线l1、l2的夹角余弦值是( )
| A. | $\frac{\sqrt{15}}{15}$ | B. | -$\frac{\sqrt{210}}{15}$ | C. | $\frac{\sqrt{210}}{15}$ | D. | -$\frac{\sqrt{15}}{15}$ |
13.在△ABC中,角A,B,C成单调递增的等差数列,a,b,c是的△ABC三边,$b=\frac{{\sqrt{3}}}{2}$,则c-a的取值范围是( )
| A. | $(0,\frac{1}{4})$ | B. | $(0,\frac{{\sqrt{3}}}{2})$ | C. | $(0,\frac{1}{2})$ | D. | ($\frac{1}{4}$,$\frac{\sqrt{3}}{2}$) |
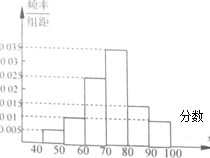 对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.
对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.