题目内容
4.已知抛物线y2=4x的焦点为F,P为抛物线上一点,过P作y轴的垂线,垂足为M,若|PF|=4,则△PFM的面积为( )| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 8 |
分析 设出P的坐标,利用抛物线的定义可知|PF|=|PM|+1,进而可求得y0,最后利用三角性的面积公式求得答案.
解答 解:由题意,设P($\frac{{{y}_{0}}^{2}}{4}$,y0),则|PF|=|PM|+1=$\frac{{{y}_{0}}^{2}}{4}$+1=4,所以y0=±2$\sqrt{3}$,
∴S△MPF=$\frac{1}{2}$|PM||y0|=$\frac{1}{2}×3×2\sqrt{3}$=3$\sqrt{3}$.
故选:A.
点评 本题主要考查了抛物线的简单应用.涉及抛物线的焦点问题时一般要考虑到抛物线的定义,考查计算能力.

练习册系列答案
相关题目
15.复数z1、z2在复平面内的对应点关于原点对称,且z1=2+i,则$\frac{({z}_{1}-1)^{2}}{|{z}_{2}+1|}$等于( )
| A. | $\sqrt{2}$i | B. | $\frac{\sqrt{10}}{5}$i | C. | $\sqrt{2}$ | D. | 4$\sqrt{2}$+3$\sqrt{2}$i |
12.已知对任意的m∈[$\frac{1}{2}$,3),不等式x2+mx+4>2m+4x恒成立,则x的取值范围是( )
| A. | (-∞,-1]∪(2,+∞) | B. | (-∞,-3) | C. | (-∞,-1]∪[2,+∞) | D. | (2,+∞) |
19.若集合A={x|1<x≤$\sqrt{3}$},B={x|0<x≤1},则A∪B=( )
| A. | {x|x>0} | B. | {x|x≤$\sqrt{3}$} | C. | {x|0≤x≤$\sqrt{3}$} | D. | {x|0<x≤$\sqrt{3}$} |
9.设复数z=$\frac{2-i}{1+i}$,则复数z的模|z|=( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | 1 | C. | 10 | D. | 2 |
5.在下列各图中,图中两个变量具有相关关系的图是( )
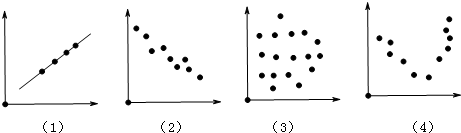

| A. | (1)(2) | B. | (1)(4) | C. | (2)(4) | D. | (2)(3) |