题目内容
16.已知定义在R上的单调递增奇函数f(x),若当0≤θ≤$\frac{π}{2}$时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,则实数m的取值范围是(-$\frac{1}{2}$,+∞).分析 根据函数的单调性和奇偶性将不等式进行转化,分离参数,确定其范围,即可得到结论.
解答 解:∵当0≤θ≤$\frac{π}{2}$时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,函数是奇函数,
∴当0≤θ≤$\frac{π}{2}$时,f(cosθ+msinθ)<f(2m+2)恒成立,
∵函数是定义在R上的单调递增函数,
∴cosθ+msinθ<2m+2,当0≤θ≤$\frac{π}{2}$时恒成立,
∴m>$\frac{2-cosθ}{sinθ-2}$
令t=$\frac{cosθ-2}{sinθ-2}$,其几何意义是P(sinθ,cosθ)(0≤θ≤$\frac{π}{2}$)与C(2,2)连线的斜率,
P点的轨迹为半径为1的单位圆,如图:
∴$\frac{1}{2}$≤t≤2,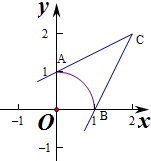
∴-2≤t≤$-\frac{1}{2}$
∴m>$-\frac{1}{2}$.
故答案为:(-$\frac{1}{2}$,+∞)
点评 本题考查函数单调性与奇偶性的结合,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.若复数(1-ai)(2+i)是纯虚数(i是虚数单位,a是实数),则a=( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
4.已知抛物线y2=4x的焦点为F,P为抛物线上一点,过P作y轴的垂线,垂足为M,若|PF|=4,则△PFM的面积为( )
| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 8 |
11.已知p:x≥5,q:x≥3,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.终边与x轴重合的角α的集合是( )
| A. | {α|α=2kπ,k∈Z} | B. | {α|α=kπ,k∈Z} | C. | {α|α=$\frac{kπ}{2}$,k∈Z} | D. | {α|α=kπ+$\frac{π}{2}$,k∈Z} |