题目内容
等差数列 的通项公式为
的通项公式为 ,下列四个命题.
,下列四个命题. :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列.其中真命题的是 .
是递增数列.其中真命题的是 .
 的通项公式为
的通项公式为 ,下列四个命题.
,下列四个命题. :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列.其中真命题的是 .
是递增数列.其中真命题的是 . ,
,
试题分析:由一次函数性质知数列
 是递增数列,所以
是递增数列,所以 为真命题;因为
为真命题;因为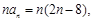 对称轴为
对称轴为 由二次函数性质知,数列
由二次函数性质知,数列 先减后增,所以
先减后增,所以 为假命题;因为
为假命题;因为 由反比例函数知,数列
由反比例函数知,数列 是递增数列,所以
是递增数列,所以 为真命题;因为
为真命题;因为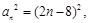 对称轴为
对称轴为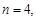 由二次函数性质知,数列
由二次函数性质知,数列 先减后增,所以
先减后增,所以 为假命题.
为假命题.
练习册系列答案
相关题目
 满足
满足 (
( 为常数,
为常数, )
) 时,求
时,求 ;
; 时,求
时,求 的值;
的值; 恒成立的常数
恒成立的常数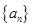 满足:
满足: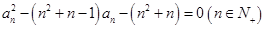 ,数列
,数列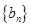 的前
的前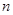 项和为
项和为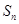 ,且满足
,且满足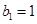 ,
,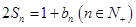 .
.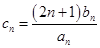 ,数列
,数列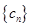 的前
的前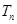 ,求证:
,求证: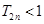 .
. 个面包分给
个面包分给 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小的
是较小的两份之和,则最小的 份为( )
份为( )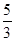

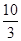

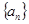 满足
满足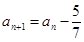 ,且
,且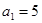 ,设
,设 项和为
项和为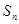 ,则使得
,则使得 ,在验证n=1成立时,等式左边是
,在验证n=1成立时,等式左边是 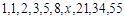 中,
中,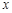 等于( )
等于( )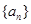 满足:
满足: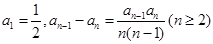 ,则该数列的通项公式
,则该数列的通项公式 =__________。
=__________。 的前n项和为
的前n项和为 ,若
,若 ,则必定有
,则必定有


